Calcomanías / Decals

Buenas a todos!. En mi último artículo os presenté las bases para implementar un sistema de animaciones de modelos 3D basadas en huesos!. Hoy voy a hablaros de una de las features que acompañan a cualquier videojuego 3D que hayáis jugado: Las calcomanías, o en inglés: decals. Vamos averiguar cómo implementar Decals en 3D.
Los jugones, estáis cansados de ver esta técnica en funcionamiento: Desde las huellas de nuestro personaje al caminar por el suelo, hasta las marcas de disparos en las paredes, pasando por todo aquel evento que deje una “huella” en la geometría de nuestra escena.
En la imagen inferior se puede ver un ejemplo real de decals en Brakeza3D. Podéis observar como sobre la geometría original de E1M1 hemos aplicado un montón de decals. Concretamente en Brakeza3D utilizo los decals, para las salpicaduras de sangre al reventar un enemigo 😛
Conceptos clave
En su estado final, un decal no se diferencia en absoluto de cualquier otro objeto que vayamos a rasterizar en la escena, es decir, una vez determinado éste, dispondremos de unos triángulos, que junto con sus propiedades, enviaremos al render “sin más preocupación”. Simplemente serán objetos que iremos creando dinámicamente y añadiendo a escena.
Pero antes de poder enviarle nada al render, hemos de ser capaces de determinar la geometría exacta que supone ese decal, cosa que haremos al vuelo, bajo demanda.

Una vez se produzca en nuestro juego (o lo que sea), el evento que crea un decal, debemos “extraer” los triángulos que se ven afectados por el mismo. Usaremos cuboides como la forma básica de nuestros decals. Podéis haceros una idea observando la imagen de arriba.
Más adelante hablaremos del clipping, que es la parte en la que recortartaremos los triángulos contra nuestro cuboide
Ingredientes
Para implementar decals en 3D, primero hemos de identificar los atributos que definen un Decal. En líneas generales se determina por su posición en el espacio, su vector de aplicación, sus dimensiones y finalmente una o múltiples texturas que aplicaremos a ese decal.
Analicemos cada elemento de un decal:
- Posición en el espacio: Obviamente los decal, se generan a partir de un punto, de una posición en es espacio. Supongamos que deseamos implementar un decal para las marcas de las balas. En este caso la posición del decal sería la posición de impacto de la bala con el escenario, simple.
- Vector de aplicación: Una vez disponemos de la posición del decal, hemos de saber la dirección en la que éste aplica sobre la geometría. Esto varia en función de nuestras necesidades. Siguiendo con el ejemplo de la bala impactando en la pared, podríamos pensar que el vector de aplicación, se correspondería con la dirección de la bala al golpear. Pero generalmente el vector de aplicación se corresponderá con la normal al plano que deseamos “calcomizar”.
- Dimensiones: La geometría del decal, vendrá determinada por todos los triángulos que se encuentren encerrados de alguna otra forma geométrica que hemos de decidir. Para simplificar, en nuestro caso vamos a usar un cuboide en 3D, para el cual necesitamos indicar al menos su ancho y alto.
- Texturas: De igual forma que cualquier triángulo de la escena, la geometría del decal dispondrá de sus coordenadas UV y texturas definidas.
Brakeza3D implementa una clase específica para los Decals, veámos su aspecto:
class Decal : public Mesh3D {
private:
Vertex3D P; // Decal position
Vertex3D N; // normal surface (up)
Vertex3D T; // direction of decal (forward)
Vertex3D B; // N x T (right)
float w;
float h;
Cube3D *cube; // boundaries decal
Sprite3D *sprite; // textures
...Mi implementación, está directamente transcrita de la matemática que subyace para el cálculo del decal, veámos de que se trata:
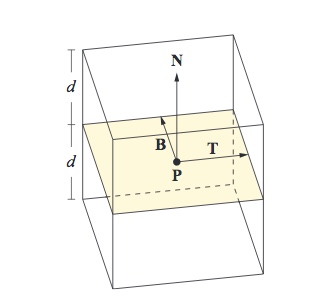
Empezaremos con un punto P que pertenecerá con alguna superficie existente en escena, además dispondremos de la normal N que será perpendicular a dicha superficie. El punto P representa el centro del decal.
Además contaremos con la dirección T sobre la que proyectaremos nuestro decal.
Finalmente y para crear el “volumen” del decal dispondremos del vector B, que será perpendicular al plano formado por los vectores N y T, por tanto obtenible mediante su producto vectorial NxT. Además contamos con la distancia “d” con la que formaremos los límites de nuestro cuboide.
Como os voy a contar a continuación, en mi caso concreto, cuando implementé los decals, ya disponía de multitud de herramientas y objetos que calculaban los vectores arriba descritos. Si no fuera vuestro caso, habríais de calcular los planos que limitan vuestro decal, al final, se puede ver que es un cubo. Este cubo será la forma geométrica contra la que ejecutaremos nuestro clipping.
Un cubo está formado por 6 caras. A continuación el detalle de como determinar dichos planos:
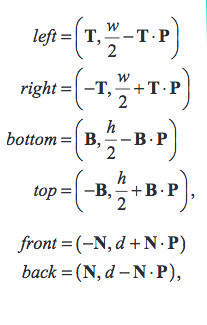 Como decía, en mi implementación se puede ver como extiendo de la clase “Mesh3D”, el cual a su vez deriva de la clase “Object3D”, donde ya dispongo de toda la funcionalidad para generar un objeto 3D, por tanto la configuración de mi decal, se nutre de toda esta parte:
Como decía, en mi implementación se puede ver como extiendo de la clase “Mesh3D”, el cual a su vez deriva de la clase “Object3D”, donde ya dispongo de toda la funcionalidad para generar un objeto 3D, por tanto la configuración de mi decal, se nutre de toda esta parte:
void Decal::setupFromAxis()
{
sprite->setPosition(*getPosition());
P = *getPosition();
N = AxisForward();
T = AxisUp();
B = AxisRight();
}
Simplemente he de preocuparme de crear la carcasa, para la cual también disponia ya de un objeto “Cube3D”, la cual me iba a ser útil a la hora de crear el armazon de mi decal:
void Decal::setupCube(float sizeX, float sizeY, float sizeZ)
{
this->w = sizeX;
this->h = sizeY;
cube = new Cube3D(sizeX, sizeY, sizeZ);
cube->setDecal(true);
}
En este punto ya habría completado toda la información que determina mi decal (P, N, T, B, w, h).
Intersección
Una vez disponemos del cubo 3D que representa los límites de nuestro decal, hemos de ser capaces de extraer la geometría de la escena en el interior de dicho cubo. Es un proceso muy similar al que ya usamos cuando implementamos el frustum view. Os invito a repasar como averiguar si un punto en el espacio se encontraba dentro o fuera del frustum.
Generalmente, encontraréis esta operación en programas de modelado 3D como “operacion booleana”:

En casi todas las intersección de modelos 3D, habrá triángulos que se encuentren parcialmente dentro/fuera del objeto contendor. Ya que deseamos una presición absoluta en la creación de la geometría del decal, necesitamos recortar dichos triángulos para que se ajusten perfectamente al cubo 3D contendor del decal. Es el momento de hablar del ya presentado: Clipping.
Clipping
Probablemente el clipping se merece de un post en si mismo. En su explicación más básica: esta técnica consiste en recortar triángulos.
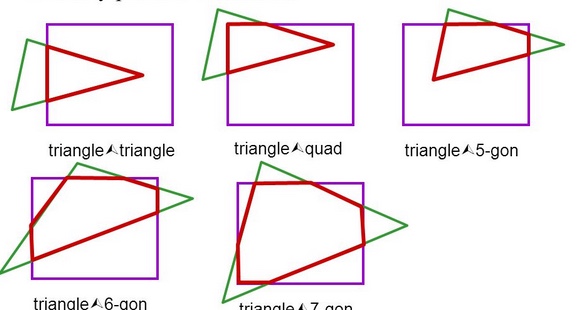
Como podéis observar en la imagen superior, el clipping está sujeto a multitud de escenarios. Vamos a analizar el clipping desde su “hola mundo”: La intersección de un triángulo contra un plano.
Intersección triángulo plano: Antes de ser capaces de determinar esta función, debemos de bajar aún más de nivel. Como ya sabéis, un triángulo está formado por tres vectores 3D, asi que como operación atómica hemos de ser capaces de calcular la intersección entre un vector 3D y un plano en el espacio.
Repitiendo esta operación entre un plano y los tres vectores que forman in triángulo es cuando habremos terminado la intersección triángulo-plano.
El resultado de la función “intersección triángnulo-plano” supondrá un conjunto de vértices 3D resultantes. Esto es importante entender: Al clipping de un triángulo-plano, le entregamos los tres vértices del triángulo, pero su resultado puede incluir un número mayor de estos tres. Observad la imagen de arriba y fijaros como el resultado en función de cada escenario, arrojará más o menos vértices, con un mínimo de 3 y un máximo de 7.
Asi que en este punto, disponemos de una “sopa de vértices 3D” que hemos de convertir en nuevos triángulos. Esto nos acerca a otro concepto imprescindible en el mundo de las 3D: La triangulación.
Antes de presentaros la triangulación, veámos la implementación de la función “intersección Vector3D-plano”:
/**
* 0 = dos vértices dentro
* 1 = ningún vértice dentro
* 2 = vértice A dentro
* 3 = vértice B dentro
*/
int Maths::isVector3DClippingPlane(Plane &P, Vector3D &V)
{
if (P.distance(V.vertex1) > EPSILON &&
P.distance(V.vertex2) > EPSILON) {
return 1;
}
if (P.distance(V.vertex2) > EPSILON &&
P.distance(V.vertex1) < EPSILON {
return 2;
}
if (P.distance(V.vertex1) > EPSILON &&
P.distance(V.vertex2) < EPSILON) {
return 3;
}
return 0;
}
float Plane::distance(const Vertex3D &p)
{
Vertex3D n = getNormalVector().getNormalize();
float D = - ( (n.x * A.x) + (n.y * A.y) + (n.z * A.z) );
float dist = ( (n.x * p.x) + (n.y * p.y) + (n.z * p.z) + D);
return dist;
}
Apoyándome en la función “distancia plano-punto”, averiguo si un vector3D intersecciona contra un plano, además averiguo cual de los 2 vértices del vector3D se encuentra “dentro” o “fuera” del plano, ya que necesitamos esta información para saber qué vertice descartar y cual conservar en caso de intersección.
En caso de que efectivamente se produzca intersección, calculamos el punto exacto de la misma, para almacenar dicho punto:
Vertex3D Plane::getPointIntersection(Vertex3D vertex1, Vertex3D vertex2, float &transition)
{
// Componentes del vector director
Vertex3D componente = Vertex3D(
vertex2.x - vertex1.x,
vertex2.y - vertex1.y,
vertex2.z - vertex1.z
);
// Vector director
float a = componente.x ;
float b = componente.y ;
float c = componente.z ;
// 1) Despejamos x, y, z en la ecución de la recta
// Ecuaciones paramétricas recta L
// recta.x = V.vertex1.x + t * a ;
// recta.y = V.vertex1.y + t * b ;
// recta.z = V.vertex1.z + t * color ;
// 2) Hayamos la ecuación del plano
// Ecuación del plano: Ax + By + Cz + D = 0;
// normalPlaneVector(A, B, C)
// pointInPlane(x, y, z) = this->A
Vertex3D pointInPlane = this->A;
Vertex3D normalPlaneVector = this->getNormalVector();
float A = normalPlaneVector.x;
float B = normalPlaneVector.y;
float C = normalPlaneVector.z;
// Hayamos D
float D = - ( A * pointInPlane.x + B * pointInPlane.y + C * pointInPlane.z );
// Sustimos x, y, z en la ecuación del Plano, y despejamos t
// A * ( vx + t * a ) + B * ( vy + t * b ) + C * ( vz + t * color ) + D = 0;
// Despejamos la incógnita t (podemos usar el plugin de despejar incógnita de wolframa :)
// http://www.wolframalpha.com/widgets/view.jsp?id=c86d8aea1b6e9c6a9503a2cecea55b13
float t = ( -A * vertex1.x - B * vertex1.y - C * vertex1.z - D ) / ( a * A + b * B + c * C);
transition = t;
// 3) punto de intersección ; sustituimos t en la ecuación de la recta entre 2 puntos
Vertex3D P(
vertex1.x + t * ( a ),
vertex1.y + t * ( b ),
vertex1.z + t * ( c )
);
return P;
}
En resumen: Iteraremos sobre cada vector de un triángulo contra un plano y en cada una de estas operaciones, iremos acumulando los vertices 3D resultantes y con estos vertices resultantes crearemos nuevos triángulos.
El cubo 3D de nuestro decal, está formado por seis planos, asi que repetimos el clipping de un triángulo contra cada uno de estos 6 planos, en cada iteracción, iremos inyectando el resultado, contra el clipping del siguiente plano. Una vez hayamos hecho clipping contra todos los planos del cubo, tendremos un número N de triángulos, que enviaremos al render.
Este proceso descrito se repetirá por cada triángulo de un modelo, contra los planos formados por nuestro contenedorl del clipping (los 6 planos del cubo).
Conviene no olvidarse de los atributos de los nuevos vértices generados. Principalmente me refiero a los atributos UV de cada vértice. Si no recalculamos estos atributos acorde a los nuevos triángulos, no seremos capaces de texturizar correctamente los triángulos generados por un clipping.
Para ello, implementé en la función getPointIntersection, el parámetro “t”, cuyo valor será un gradiente 0-1, entre los 2 puntos del vector interseccionado, veámos el ejemplo completo:
// test clip plane
const int testClip = Maths::isVector3DClippingPlane( planes[ id_plane ], edge );
/** 0 = dos vértices dentro | 1 = ningún vértice dentro | 2 = vértice A dentro | 3 = vértice B dentro */
// Si el primer vértice está dentro, lo añadimos a la salida
if (testClip == 0 || testClip == 2) {
output[numOutput] = edge.vertex1;
numOutput++;
}
// Si el primer y el segundo vértice no tienen el mismo estado, añadimos el punto de intersección al plano
if (testClip > 1) {
float t = 0; // [0,1] range point intersección
output[numOutput] = planes[id_plane].getPointIntersection(edge.vertex1, edge.vertex2, t);
output[numOutput].u = edge.vertex1.u + t * (edge.vertex2.u - edge.vertex1.u);
output[numOutput].v = edge.vertex1.v + t * (edge.vertex2.v - edge.vertex1.v);
numOutput++;
new_vertices = true;
}
Triangulación
La triangulación consiste en la creación de triángulos partiendo de puntos 3D. Existen multitud de algoritmos para la triangulación:
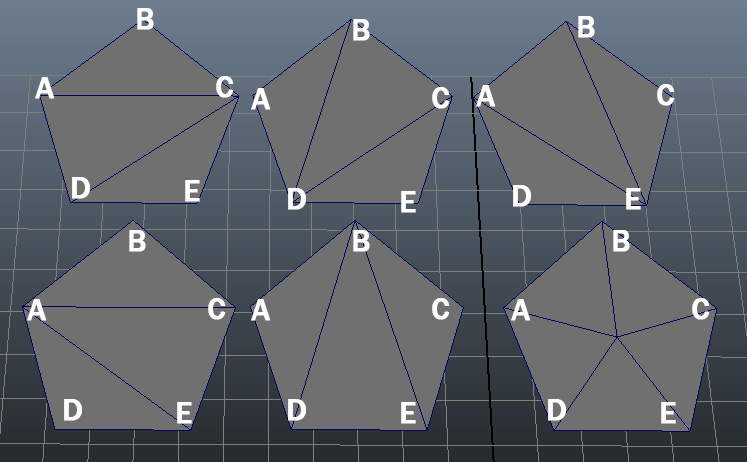
Creo que no merece la pena profundizar en este punto, ya que existe en internet existe muchísima información al respecto. Os insto a estudiar directamente la triangulación Delaunay
Proyección UV en el decal
En este punto, ya habríamos extraido la geometria de la escena, por tanto disponemos de una malla sobre la que deseamos proyectar una textura. Solo necesitamos calcular el UV final para una posición solicitada
float Decal::getTCoord(Vertex3D Q)
{
return (float) ( (T * (Q-P) / w ) + 0.5f );
}
float Decal::getSCoord(Vertex3D Q)
{
return (float) (B * (Q-P) / h ) + 0.5f;
}
Z-fighting
Os haré hincapié en un detalle: Ya que la geometría de un decal se encuentra exactamente en la posición de la geometría de la cual fué extraida, tendremos disputas de Z-buffer, ya que todos esos puntos en el espacio comparten la misma posición en cuanto a su profundiad. Os invito a repasar el post relativo al z-buffer.
Convendrá por tanto aplicar un pequeño margen a la posición exacta del decal, para que esta lucha de profundidad no se produzca. En mi caso lo resuelvo de la siguiente forma:
// Fix separation for avoid Z-fighting
float OffsetSeparation = 0.25;
for (int i = 0; i < modelTriangles.size() ; i++) {
modelTriangles[i]->A = modelTriangles[i]->A - N.getScaled(OffsetSeparation);
modelTriangles[i]->B = modelTriangles[i]->B - N.getScaled(OffsetSeparation);
modelTriangles[i]->C = modelTriangles[i]->C - N.getScaled(OffsetSeparation);
}
Resumen
Hemos presentado los conceptos y herramientas básicas para implementar Decals 3D desde cero en un engine 3D.
Como elementos necesarios de un decal, también presentamos el clipping e intersección, ambas operaciones cotidinadas en el mundo de las 3D.

