Frustum

Vamos a dar otro paso en la dirección de convertirnos en desarrollador de videojuegos.

Hoy vamos a presentar el Frustum!. Es un concepto que encontrareis en cualquier motor y representa el espacio en el mundo al alcance del campo de visión de nuestra cámara. Desde el punto de vista geométrico, el frustum equivale a una pirámide truncada.

El objetivo habitual del frustum view, es descartar toda la geometría que se encuentra fuera. Con este paso, evitaremos los cálculos para las transformaciones de los vértices y la posterior rasterización de triángulos que no se encuentran visibles. Sin embargo el frustum sirve para más cosas.

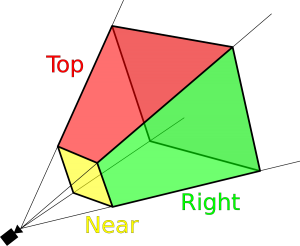
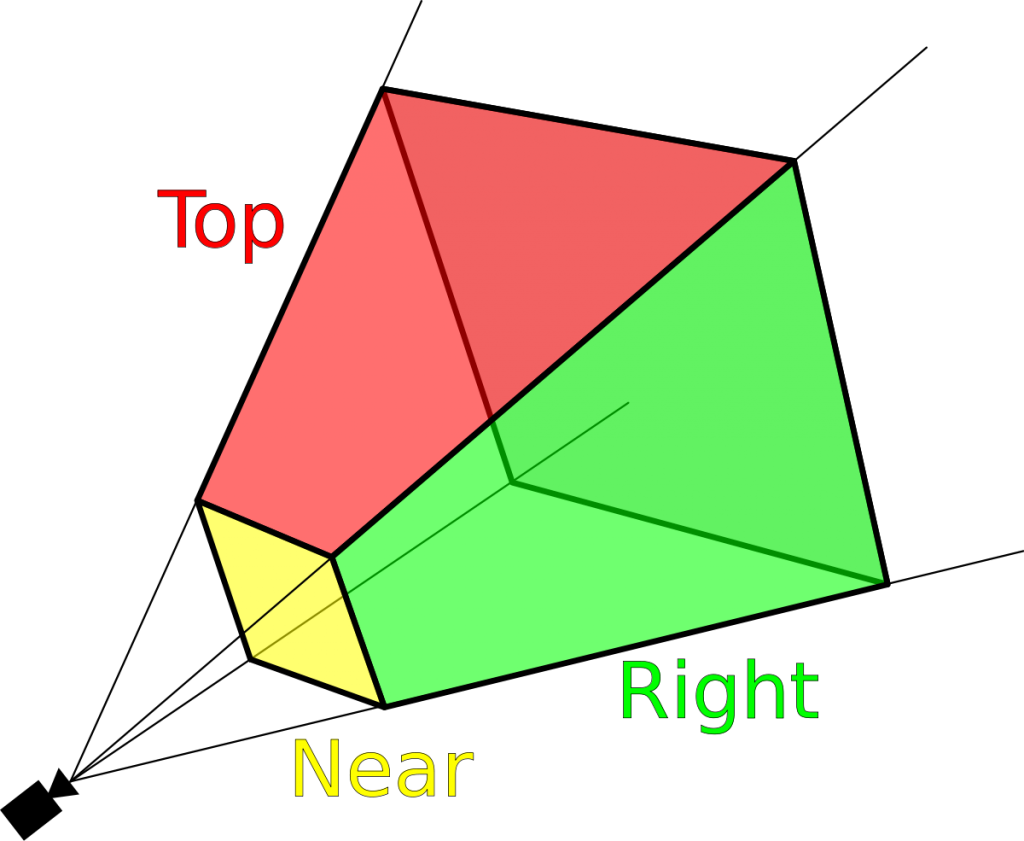
Como podeis observar en la imagen superior, el Frustum se define a través de seis planos. De todos ellos, cabe destacar el “Near” y “Far” planes, el plano mas cercano y el mas lejano respecto a la posición de la cámara.

Por ahora, nuestro primer objetivo será como averiguar los planos que conforman nuestro Frustum.

Observemos el código que configura el Frustum para la cámara en Brakeza3D.

void Frustum::setup(Vertex3D position, Vertex3D direction, Vertex3D up, Vertex3D right, float nearDist, float Hnear, float Wnear, float farDist, float Hfar, float Wfar)
{
    this->position = position;
    this->direction = direction;
    this->up = up;
    this->right = right;

    this->nearDist = nearDist;
    this->farDist = farDist;

    this->Hnear = Hnear;
    this->Wnear = Wnear;

    this->Hfar = Hfar;
    this->Wfar = Wfar;
}

Apenas con unas líneas de código nuestro Frustum queda determinado. Vamos a razonar cada uno de sus propiedades. Si tomamos como referencia la imagen inferior, observamos que los planos de la pirámide se forman con ocho vértices:

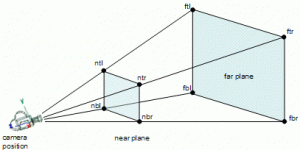
Os adelanto, que estos vértices deben ser recalculados constantemente, al menos, cada vez que nuestra cámara se mueva por el espacio.

Por tanto, necesitamos algunos datos y puntos referencia a partir de los cuales podremos obtener estos ocho vértices para finalmente, hayar sus planos y lados.

Prestad atención a la siguiente imagen:

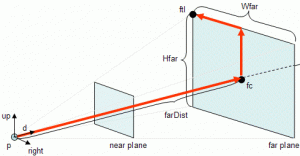
Se puede ver que el frustum se origina en un punto en el espacio (p), que en nuestro caso se corresponde con la posición de la cámara. Desde ese punto ,el frustum “mira” hacia una dirección concreta (d). Si trazásemos un rayo en dicha dirección, éste chocaría en dos puntos contra el frustum, uno en el centro del plano cercano cercano (nearCenter) y otro en el centro del plano lejano (farCenter). La distancia a la que chocan estos puntos viene determinada por su distancia a la cámara, llamaremos a estas distancias nearDist y farDist. Una vez conocemos los puntos en el espacio del nearCenter y el farCenter, nos apoyaremos en los vectores Up y Right conjuntamente con los tamaños de estos planos: widthNear, heightNear y widthFar, heightFar. Los vectores Up y Right, mantendrán los planos near y far paralelos y alineados correctamente.

En la práctica eso se resuelve con pocas líneas de código:

void Frustum::updateCenters() {
    // far center
    fc.x = this->position.x + direction.x * farDist;
    fc.y = this->position.y + direction.y * farDist;
    fc.z = this->position.z + direction.z * farDist;

    // near center
    nc.x = this->position.x + direction.x * nearDist;
    nc.y = this->position.y + direction.y * nearDist;
    nc.z = this->position.z + direction.z * nearDist;
}

Os recomendaría familiarizaros con la fórmula:

P = O + V * t

Lo que esto hace en resumen, es sumarle a un punto origen otro vector de tamaño “t” en la dirección de V. Lo encontrareis en muchos sitios.

Es importante recordar que los vectores dirección (d), Up  y Right deben ser normalizados, es decir, de longitud 1. Podeis encontrar el código para normalizar un vector en el repositorio de Brakeza3D.

Una vez hemos calculado los centros de nuestro Near y Far plane, podemos continuar con el resto:

void Frustum::updatePoints() {
    ntl.x = nc.x + (up.x * Hnear/2) - (right.x * Wnear/2);
    ntl.y = nc.y + (up.y * Hnear/2) - (right.y * Wnear/2);
    ntl.z = nc.z + (up.z * Hnear/2) - (right.z * Wnear/2);

    ntr.x = nc.x + (up.x * Hnear/2) + (right.x * Wnear/2);
    ntr.y = nc.y + (up.y * Hnear/2) + (right.y * Wnear/2);
    ntr.z = nc.z + (up.z * Hnear/2) + (right.z * Wnear/2);

    nbl.x = nc.x - (up.x * Hnear/2) - (right.x * Wnear/2);
    nbl.y = nc.y - (up.y * Hnear/2) - (right.y * Wnear/2);
    nbl.z = nc.z - (up.z * Hnear/2) - (right.z * Wnear/2);

    nbr.x = nc.x - (up.x * Hnear/2) + (right.x * Wnear/2);
    nbr.y = nc.y - (up.y * Hnear/2) + (right.y * Wnear/2);
    nbr.z = nc.z - (up.z * Hnear/2) + (right.z * Wnear/2);

    ftl.x = fc.x + (up.x * Hfar/2) - (right.x * Wfar/2);
    ftl.y = fc.y + (up.y * Hfar/2) - (right.y * Wfar/2);
    ftl.z = fc.z + (up.z * Hfar/2) - (right.z * Wfar/2);

    ftr.x = fc.x + (up.x * Hfar/2) + (right.x * Wfar/2);
    ftr.y = fc.y + (up.y * Hfar/2) + (right.y * Wfar/2);
    ftr.z = fc.z + (up.z * Hfar/2) + (right.z * Wfar/2);

    fbl.x = fc.x - (up.x * Hfar/2) - (right.x * Wfar/2);
    fbl.y = fc.y - (up.y * Hfar/2) - (right.y * Wfar/2);
    fbl.z = fc.z - (up.z * Hfar/2) - (right.z * Wfar/2);

    fbr.x = fc.x - (up.x * Hfar/2) + (right.x * Wfar/2);
    fbr.y = fc.y - (up.y * Hfar/2) + (right.y * Wfar/2);
    fbr.z = fc.z - (up.z * Hfar/2) + (right.z * Wfar/2);
}

Con esto, hemos terminado el cálculo de nuestros ocho vértices. Ahora solo falta agruparlos correctamente para formar nuestros planos. Un plano, queda determinado de varias maneras, una de ellas es con al menos tres puntos del mismo, que es nuestro caso:

// near/far plane
planes[NEAR_PLANE]   = Plane(ntl, ntr, nbl);   // near
planes[FAR_PLANE]    = Plane(ftr, ftl, fbl);   // far

// view frustum
planes[LEFT_PLANE]   = Plane(position, fbl, ftl  );   // left
planes[RIGHT_PLANE]  = Plane(position, ftr, fbr );   // right
planes[TOP_PLANE]    = Plane(position, ftl, ftr );   // top
planes[BOTTOM_PLANE] = Plane(position, fbr, fbl );   // bottom

Como veis, hemos añadido la clase Plane, a la que le iremos añadiendo métodos poco a poco. Será útil, obtener el plano formado por un triángulo.

Cabe mencionar, que la mayor parte de librerías de gráficos, por ejemplo OpenGL, incluyen sus propias funciones para la creación del Frustum de forma ultra-optimizadas por hardware, sin embargo, los parámetros que determinan un frustum suelen ser los que hemos descrito, os invito a comprobarlo por vosotros mismos!

¿Y cómo uso el frustum?

En una segunda fase, nos interesará comprobar si nuestros triángulos se encuentran en el interior del frustum, en caso contrario, sabremos que podemos descartar dicho triángulo de la rasterización.

Algunos ya estaréis pensando, que habrá triángulos que NO estén completamente fuera, ni completamente dentro del frustum, es decir, que serán “cortados” por éste. Efectivamente, esto sucede constantemente cuando renderizamos entornos con un mínimo de tamaño. Esto nos lleva a otro concepto: el Clipping. Hablaremos en otro post sobre el Clipping, por ahora nos limitaremos a descartar triángulos que no estén completamente dentro del frustum.

El primer paso para comprobar si un triángulo está dentro del frustum, es tener la capacidad de comprobar si un solo vértice está dentro o no del frustum.

Como ya he dicho, el frustum está compuesto de 6 planos. Estos planos, forman un espacio cerrado, que es el espacio contra el que que nos interesa comprobar nuestro vértice. Antes de nada, imaginemos un plano y un punto en el espacio: Existen tres posibilidades

• El punto está a la izquierda del plano
• El punto está a la derecha del plano
• El punto está exactamente en el plano

En la práctica, esto se consigue calculando la distancia entre el punto y el plano, pudiendo ésta ser negativa. Por tanto, la distancia podrá ser cero, negativa o positiva. Con este sencillo mecanismo, aplicado a cada plano, podremos saber si un vértice está encerrado el frustum.

Observemos la función que he utilizado para medir esta distancia, es para perderle el respeto:

float Plane::distance(const Vertex3D &p) {
    Vertex3D n = getNormalVector().getNormalize();

    float D = - ( (n.x * A.x) + (n.y * A.y) + (n.z * A.z) );
    float dist = ( (n.x * p.x) + (n.y * p.y) + (n.z * p.z) + D);

    return dist;
}

Os recomiendo encarecidamente revisar el post anterior en el que os presento algunos libros, que me ayudaron mucho a consolidar estas fórmulas.

Para entender el código de arriba, se necesita primero entender el concepto de “vector normal” de un plano, que no deja de ser un vector perpendicular al mismo.

Además se hace uso de la ecuación del plano: Ax + Bx + Cx + D = 0

Cuando veais la ecuación del plano, recordad que A, B y C, son las componentes X, Y y Z del vector normal del plano, las cual conoceréis y donde x, y y z, son las coordenadas de un punto perteneciente al plano (en el caso de un triángulo, ya tenéis 3 a elegir). Con esta información podríais despejar el término independiente D para finalmente, averiguar la distancia.

Para calcular el vector normal al plano, nos apoyaremos en el hecho (me repito!), de que nuestro plano “nace” de un triángulo, es decir, ya disponemos de tres vértices (no alineados), que sabemos que forman parte del plano. Con estos tres vértices, podemos formar al menos dos vectores y calcular su cross product, una operación cuyo resultado nos entrega un vector perpendicular a estos.

Aquí se puede observar el código que realiza el cross product entre dos puntos en el espacio:

Vertex3D Vertex3D::operator %(const Vertex3D &v) {
    Vertex3D V;

    V.x = (this->y * v.z) - (this->z * v.y);
    V.y = (this->z * v.x) - (this->x * v.z);
    V.z = (this->x * v.y) - (this->y * v.x);

    return V;
}

Con estas herramientas implementadas, podemos continuar, para completar nuestra función que comprobará si un vértice se encuentra dentro o no de los planos del frustum:

bool Frustum::isPointInFrustum(Vertex3D v) {

    bool result = true;
    int plane_init = engine::get()->FAR_PLANE;
    int plane_end = engine::get()->BOTTOM_PLANE;

    for(int i = plane_init; i <= plane_end; i++) {
        if (planes[i].distance(v) >= engine::get()->EPSILON) {
            return false;
        }
    }
    return result;
}

Como un triángulo tiene tres vértices, hacemos tres comprobaciones para cada vértice, si alguno no está dentro, descartaremos dicho triángulo:

if (!cam->frustum->isPointInFrustum(Ao) &&
    !cam->frustum->isPointInFrustum(Bo) &&
    !cam->frustum->isPointInFrustum(Co)
) {
    EngineBuffers::get()->trianglesOutFrustum++;
    return false;
}

Con esto, hemos terminado la fase en la que descartamos geometría fuera del frustum!.  Es una gran (y obligada) optimización!

Algunos, os preguntaréis la utilidad del valor EPSILON en la función de la distancia. Como habréis observado, en lugar de comprobar contra el valor 0.0f, lo hacemos contra un valor que consideraremos el mínimo aceptable para considerar la comprobación por válida. En mi caso utilizo 0.005f. Se trata de darle cierta holgura. En algún post os hablaré sobre la robustez numérica.

El Near Plane

Hasta ahora, nos hemos centrado en la faceta de “optimización” del frustum, utilizándolo para descartar triángulos que no nos interesa llevar hasta la fase de rasterización. Sin embargo, me parece interesante aprovechar que hemos presentado el Near Plane, para profundizar en su naturaleza.

No nos hemos detenido demasiado en las variables nearDist y farDist, que se correspondían con las distancias de cada plano al punto de la cámara. Observad la siguiente imagen:

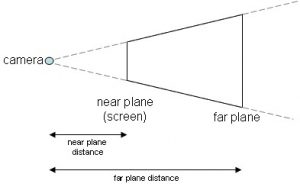
Hasta ahora, hemos hablado del frustum de forma genérica, enumerando los datos que determinan un Frustum en el espacio, sin embargo, deseamos que nuestro frustum se adapte a las necesidades de nuestro motor 3D. No sirve cualquier configuración arbitraria. En la imagen superior, podeis encontrar un dato clave: El Near Plane se corresponde con nuestra pantalla (screen),  la cual tiene un tamaño fijo.

El frustum que se origina en la posición de la cámara y cuyo Near Plane está sincronizado con nuestra pantalla se suele denominar Frustum-View.

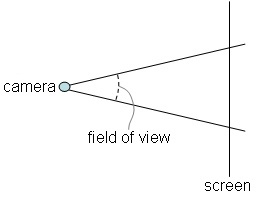
Si el tamaño de nuestro Near Plane viene determinado por nuestra pantalla, no podemos decidir cambiar el ancho y alto del mismo cuando queramos. Simplemente podemos calcular su tamaño y adaptarnos a éste. No olvidéis esto!

Nos acercamos a un concepto interesante, el campo de visión (field of view). El valor de nearDist, colocará el Near Plane más o menos lejos de la posición de la cámara, asi que el ángulo del campo de vista se verá afectado. Si nos apoyamos en la imagen superior, e imaginamos el punto de la cámara mas cerca del plano (nearDist mas pequeño), el ángulo del campo de vista se incrementa, si por el contrario imaginamos el punto de la cámara mas lejos (nearDist mas grande), el campo de vista se reduce.

Para abreviar, utilizaremos FOV para referirnos al campo de vista. Además, podemos razonar, que existen dos tipo: un FOV horizontal y un FOV vertical. Esto se debe a que nuestro Near Plane (pantalla), no es cuadrado, si lo fuera, podríamos trabajar solamente con un FOV.

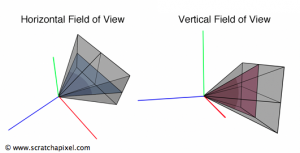
Como véis, el FOV vertical y horizontal están estrechamente relacionados, no puedes alterar uno, sin que el otro se vea afectado. A su vez, los FOV están estrechamente relacionados con la distancia para nearDist.

Lo que haremos será decidir el ángulo deseado para el FOV horizontal (este será el único parámetro que podemos decidir arbitrariamente), con esto, podremos determinar el valor de nearDist, para finalmente averiguar el FOV vertical. Con toda esta información, podremos determinar las dimensiones del Near Plane en el espacio.

¿Cuál debe ser el valor de nearDist?

Como os acabo de indicar, el valor de nearDist vendrá determinado en función del FOV horizontal elegido. Éste valor en los juegos, suele ser de 90, es decir, nuestro campo de visión es de 90º, 45º hacia la izquierda y 45º hacia la derecha. El valor de 90, no es casual, se trata de una comodidad inicial. Veámos las siguientes imágenes:

FOV Horizontal:

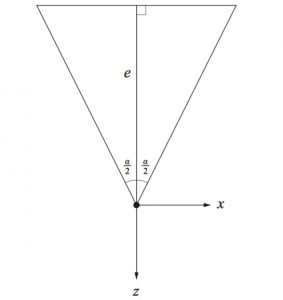
Si desarrollamos los triángulos de las imágenes superiores, veremos que si el FOV horizontal es de 90º, la distancia de la cámara al nearPlane será uno:

float Camera3D::getNearDistance() {
    return (1 / tanf( Maths::degsToRads(this->horizontal_fov/2) ));
}

Os invito a comprobarlo por vosotros mismos!

Para hayar el FOV vertical, será necesario presentar el concepto de “Aspect Ratio“, que no es mas que la relación entre el alto y el ancho de nuestra pantalla, por tanto una constante. Si por ejemplo, nuestra pantalla tiene una resolución de 640×480, su aspect ratio, será de 0.75.

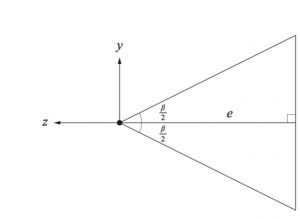
Una vez conocemos el aspect ratio para nuestra pantalla, podemos determinar el FOV vertical

float Camera3D::getVerticalFOV() {
    float vfov = 2 * atanf( getAspectRatio() / getNearDistance() );

    return Maths::radsToDegs( vfov );
}

Ya casi estamos!. Sólo nos falta averiguar las dimensiones de nuestro Near y Far Planes, para poder construir nuestro Frustum View (frustum aplicado a la cámara).

float Camera3D::calcCanvasNearWidth() {
    float width = ( 2 * tanf( Maths::degsToRads(horizontal_fov / 2) ) * getNearDistance() ) ;

    return width;
}

float Camera3D::calcCanvasNearHeight()
{
    float height = ( 2 * tanf( Maths::degsToRads( getVerticalFOV() / 2) ) * getNearDistance() ) * getAspectRatio();

    return height;
}

Hemos terminado!. Con toda esta información, deberíamos ser capaces de configurar nuestro Frustum-View en el espacio siempre que necesitemos. Éste frustum, tendrá un Near Plane perfectamente adaptado a nuestra pantalla.

En un siguiente post, profundizaremos aún más en la utilidad de éstos planos del frustum view, ya que serán necesarios para una transformación del pipeline estándar que nos habíamos saltado en el post sobre “Creando nuestra primera cámára virtual“.

Resumen

Hemos presentado algunas técnicas para construir un Frustum en el espacio, además de presentar los cálculos para configurar un Frustum View integrado con nuestra cámara.

Además, hemos aprendido a comprobar cuando un triángulo se encuentra en el interior del frustum, lo cual supone una optimización prácticamente obligada.

En el siguiente post, avanzaremos en la implementación de nuestra cámara virtual con lo aprendido aquí. Nos vemos!