Con lo aprendido en los artículos anteriores, seríamos capaces de llevar la geometría de un objeto (compuesto por vértices) a la pantalla de nuestro ordenador, mediante una malla de triángulos formada por líneas rectas, además, podríamos mover y rotar dicha geometría en el espacio. Grandes avances para tan poca teoría pensarán algunos!!.
De todas formas, nuestro motor 3d todavía carece de alguna de las funciones mas básicas, como por ejemplo, una cámara.
En Internet, existe multitud de información para explicar como funciona una cámara 3D. En ocasiones comienzan hablando de conceptos de física, sobre la luz y sus características, lo que nos adentran en un mundo que puede abrumarnos inicialmente. Intentaremos evitar este enfoque tan académico por ahora y resumiremos que una cámara es un punto y una dirección en el espacio.
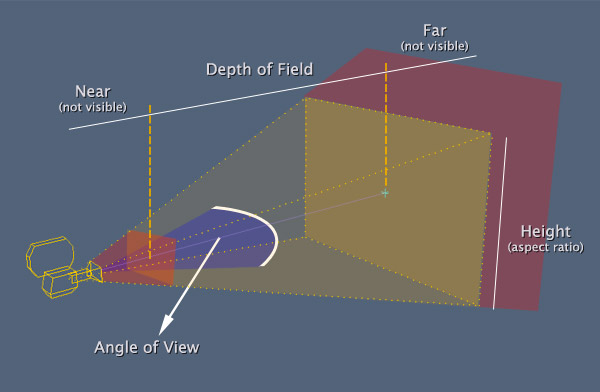
Se puede observar en la imagen superior, que hay varios elementos que intervienen en el funcionamiento completo de una cámara 3D. Como advertencia, decir que la implementación completa de nuestra cámara, requerirá de varios capítulos en los que iremos añadiendo capacidades a la misma, presentando la naturaleza de cada término y su utilidad (fov, near plane, etc).
Los requisitos mas básicos que se le piden a una cámara, son el movimiento y la rotación. Hemos de ser capaces de movernos por la escena, es decir, avanzar o retroceder y subir o bajar además de girar la dirección a la que enfocamos, todo ello a nuestro antojo. Por ahora este será nuestro objetivo, una vez alcanzado, nos detendremos con la cámara y profundizaremos otros aspectos del motor antes de retomarla.
Antes de continuar en materia os invito a una simple reflexión: Dado que ya sabemos mover y rotar objetos, ¿que pasaría si en lugar de preocuparnos por cómo mover la cámara, nos limitamos a mover y a rotar TODOS los objetos de la escena?. Si la montaña no viene a Mahoma, Mahoma va a la montaña. Efectivamente la sensación visual en movimiento, sería la deseada.
Para digerir con facilidad el resto de artículos que vendrán os sugiero manejar con soltura lo que viene a continuación. Analizaremos la vida de un vértice en nuestro motor 3d.
Espacios de coordenadas
Hasta ahora en nuestros ejemplos de código, el ciclo de vida de un vértice apenas tenía dos partes, una, desde que leíamos su información en el espacio (x, y, z), y dos, cuando lo transformábamos a su homólogo en dos dimensiones.
Para implementar una cámara virtual será necesario ampliar este ciclo de vida añadiendo mas partes, cada una con un fin y cálculos específicos. A continuación os presento el «pipeline» habitual para las transformaciones de un vértice en cualquier engine 3D:
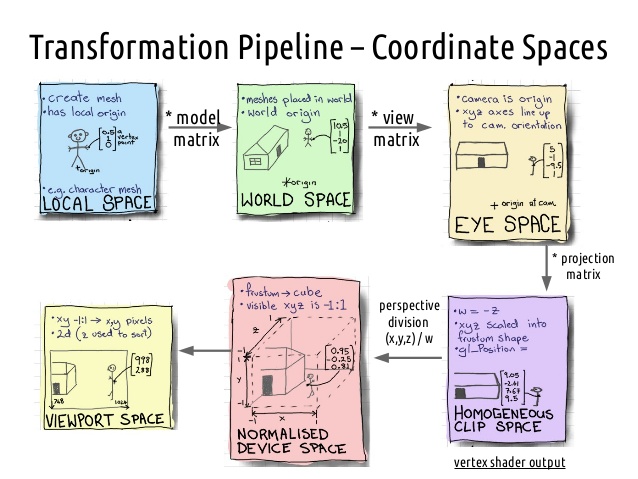
Se puede observar que este ciclo está compuesto por seis transformaciones, lo que amplia notablemente la propuesta de nuestros ejemplos hechos hasta ahora. Hoy vamos a analizar las tres primeras transformaciones básicas y la última:
Local Space: El espacio local de un vértice se corresponde con su información en bruto, la cual está referida a su propio origen de coordenadas. Imaginad los 8 vértices de un cubo exportado desde Blender, entre ellos mismos, están en su propio espacio, de ahí lo de «local».
World Space: Imaginemos los 8 vértices del cubo anterior. Si deseo posicionar ese cubo en cualquier punto del mundo en tres dimensiones debo aportarle una posición, la cual será tomada como punto de origen para posicionar los vértices con la información de su espacio local. De esta manera podríamos aprovechar los datos del cubo (modelo 3d) para instanciarlo en diferentes objetos en nuestra escena, cada uno con su posición en el mundo.
Eye Space: También llamado «Camera Space». Diremos que un vértice está en espacio de cámara cuando su posición tiene a la cámara como origen de coordenadas. En otras palabras, el «Eye Space» almacena la información de los vértices respecto a la posición de la cámara.
Viewport Space: El último paso y donde finalmente convertiremos nuestro punto 3D en 2D para dibujarlo en nuestra pantalla. Único momento en el que pasaremos a manejar solo dos componentes: x e y.
Con este panorama por ahora podemos solventar de forma ordenada el reto de mover y rotar una cámara a nuestro antojo, ademas prepararemos el camino para hablar de las dos fases que nos hemos dejado en el tintero: NDC (Normalised Device Space ) y HCS (Homogeneous Clip Space).
Vamos al lio
Nuestra primer cámara 3D
Es el primer ejemplo en el que haremos uso de la programación orientada a objetos.
Crearemos un conjunto de clases para encapsular todo lo que necesita esta evolución de nuestro motor. Estas serían: Camara3D, Object3D, Vertex3D y Point2D. Además necesitaremos métodos para transformar vértices de un espacio de coordenadas a otro.
Finalmente, implementaremos una simple captura de teclado para manipular nuestra cámara virtual y conseguir movernos por la escena.
Hagamos un repaso a nuestra nueva arquitectura de clases:
Vertex:
class Vertex {
public:
float x, y, z;
};Object3D:
class Object3D {
public:
Vertex position;
float rotX, rotY, rotZ;
};Camera3D (nótese que es una derivada de Object3D, la dirección de la cámara será el ejeZ de su Object3D, no necesitamos mas):
class Camera3D : public Object3D {
};Point2D:
class Point2D {
public:
int x;
int y;
};Este simple esquema de clases será suficiente por ahora. Vamos a ver las funciones que necesitaremos para transformar vértices. A continuación la forma de obtener las coordenadas de mundo de un vértice:
Vertex objectSpace(Vertex A, Object3D *o)
{
Vertex v = A;
v = rotarEjeX(v, o->rotX);
v = rotarEjeY(v, o->rotY);
v = rotarEjeZ(v, o->rotZ);
v = addVertex(v, o->position.x, o->position.y, o->position.z);
return v;
}La forma de obtener las coordenadas de cámara, partiendo de las coordenadas de mundo:
Vertex cameraSpace(Vertex V, Camera3D *cam)
{
Vertex A = V;
A = subVertex(A, cam->position.x, cam->position.y, cam->position.z);
A = rotarEjeX(A, cam->rotX);
A = rotarEjeY(A, cam->rotY);
A = rotarEjeZ(A, cam->rotZ);
return A;
}Para las coordenadas de pantalla hemos simplemente renombrado el ejemplo de la funcion que hemos venido usando para convertir puntos 3D a 2D:
Point2D screenSpace(Vertex v, Camera3D *cam)
{
Point2D A;
A.x = (int) v.x;
A.y = (int) v.y;
if (v.z != 0 ) {
A.x = v.x / v.z;
A.y = v.y / v.z;
}
return A;
}La captura de teclado la haremos mediante los mecanismo que ofrece SDL para recepción de inputs. Concretamente utilizaremos los cursores para modificar la posición de nuestra cámara. Adaptaremos nuestro Main Loop de la siguiente forma:
while(!finish) {
while (SDL_PollEvent(&event)) {
processObject3D()
if (event.type == SDL_KEYDOWN) {
switch (event.key.keysym.sym) {
case SDLK_UP:
break;
case SDLK_DOWN:
break;
case SDLK_LEFT:
break;
case SDLK_RIGHT:
break;
}
}
}
SDL_RenderPresent(renderer);
}Hemos añadido un par de funciones, addVertex y subVertex que simplemente suman y restan valores a las magnitures de un vértice.
Con estas piezas tenemos todo lo necesario para articular nuestra primer cámara 3D virtual. Hemos de procesar cada vértice 3D en nuestro pipeline, que por ahora consiste en las funciones: objectSpace, cameraSpace y screenSpace. En cada iteración por nuestro main-loop, todos los vértices serán procesados por estas funciones.
Ya que el cálculo de estos espacios de coordenadas utiliza la posición y rotación de la cámara, a medida que modifiquemos éstos valores, estaremos modificando la representación final en el espacio 2D (screenSpace) y con ello el efecto deseado. Por ahora hemos terminado!
Resumen
Estrictamente hablando no hemos aportado ningúna novedad técnica en este artículo: Ya sabíamos mover y rotar vértices en 3D, podríamos haber simulado una cámara 3D utilizando ambas técnicas.
Sin embargo hemos presentado los espacios de coordenadas, conceptos que hemos de manejar con soltura para el futuro. Es interesante adquirir la visión de «pipeline» como un conjunto de operaciones que realizaremos siempre en todos los vértices y en el mismo orden.
Además hemos creado una arquitectura de objetos (Vertex, Object3D, Camera3D, Point2D) que nos permitirá extender nuestro motor con cierta comodidad durante los próximos capítulos. Finalmente hemos integrado todo en un main-loop que modifica la posición de la cámara mediante captura de teclado.
Hasta que hablemos del Frustum View en artículos posteriores, no profundizaremos mas en nuestra cámara 3D, nos conformamos con poder movernos (posición/rotación) por nuestro mundo 3D.





Deja una respuesta