Con lo tratado en el articulo anterior, hemos visto como mover y rotar vértices en el espacio. Si aplicamos estas técnicas al conjunto de vértices de un objeto, estamos moviendo y/o rotando ese objeto. Genial!.
 Para obtener un mínimo de realismo, vamos a dotar a nuestros vértices en el espacio de una malla que los conecte.
Para obtener un mínimo de realismo, vamos a dotar a nuestros vértices en el espacio de una malla que los conecte.
Es realmente una tarea sencilla. Simplemente hemos de trazar líneas rectas de un punto A a un punto B, en un espacio en 2D. En la fase en al que dibujaremos nuestras líneas rectas, ya conoceremos la posición de nuestro punto en 2D. Este asunto lo hemos tratado en el artículo Introducción a las 3D.
Es por tanto un problema que nada tiene que ver con las tres dimensiones. La solución, si queréis ir al grano, está en la ecuación de la recta. Aunque existen algoritmos optimizados para cumplir esta tarea, vamos a hacer nuestro propio desarrollo.
Si imaginamos una recta, es sencillo comprender el concepto de pendiente. La pendiente, no es mas que el grado de inclinación de la recta, en otras palabras, la relación entre X e Y.
La forma de calcular la pendiente de una recta entre dos puntos, es la división entre el tamaño vertical y el horizontal de la misma. Con la pendiente, conocemos «cuanto incrementa Y respecto de X».
float y_diff = b.y - a.y;
float x_diff = b.x - a.x;
// m = pendiente
float m = (y_diff/x_diff);Una vez conocemos la pendiente, estamos en disposición de recorrer la distancia en el ejeX de los puntos origen y destino:
for (int i = a.x; i < b.x; i++) {
int px = i;
int py = m * (px-a.x) + a.y;
SDL_RenderDrawPoint(renderer, px, py);
}Se puede observar que este bucle, empieza en la coordenada x del punto origen, y en cada iteración averigua la posición de Y utilizando la pendiente y el valor actual de X.
Multiplicar la pendiente por el número de iteracción, nos aporta el incremento de Y a medida que avanza X:
m * (px-a.x)Lo que hace la fórmula completa, es sumar a la posición Y original del punto, el incremento que determina su pendiente.
m * (px-a.x) + a.yDetalles a tener en cuenta:
Siempre vamos a pintar nuestras líneas de izquierda a derecha: Según la posición del punto origen y destino en una línea, habrá casos en los que el punto final estará a la izquierda y otros en los que esté a la derecha del origen. Segun esto y si decidiéramos empezar siempre en el punto origen hacia el punto destino, habrá veces que debamos pintar pixeles hacia la izquierda y a veces hacia la derecha. La forma en la que resolveremos este problema será utilizando siempre el punto mas a la izquierda como el punto origen y el mas a la derecha como el punto final. Por esto en ocasiones será necesario invertir los vértices:
if (x1 > x2) {
x1 = this->x2;
y1 = this->y2;
x2 = this->x1;
y2 = this->y1;
}Si juntamos todas las piezas tenemos que:
point2d a, b;
a.x = 10; a.y = 10;
b.x = 500; b.y = 300;
float y_diff = b.y - a.y;
float x_diff = b.x - a.x;
// m = pendiente
float m = (y_diff/x_diff);
for (int i = a.x; i < b.x; i++) {
int px = i;
int py = m * (px-a.x) + a.y;
SDL_RenderDrawPoint(renderer, px, py);
}
SDL_RenderPresent(renderer);Cuyo resultado sería el siguiente:

El resultado es aceptable. Pero esconde algunos defectos. Hemos pintado una recta entre a(10, 10) y b(500, 300), repitamos la operación aumentando drásticamente la pendiente, por ejemplo a(10, 10) y b(30, 300). El resultado se convierte en este:

Se puede observar como el resultado no es el deseado, ya que nuestra línea recta no tiene continuidad. Esto es debido a que la pendiente es muy alta, por cada pixel que avanza en el ejeX, supone muchos pixeles de avance en el ejeY, lo que genera este efecto.
La solución, será añadir una pasada extra a nuestra línea, invirtiendo los ejes, es decir, además de recorrer la línea en el ejeX, lo haremos en el ejeY. Entre ambas pasadas, se pintarán todos los píxeles de nuestra línea:
Este sería el código en el que se ve como la línea se recorre en horizontal y luego en vertical:
point2d a, b;
a.x = 10; a.y = 10;
b.x = 30; b.y = 300;
float y_diff = b.y - a.y;
float x_diff = b.x - a.x;
// m = pendiente
float m = (y_diff/x_diff);
// izquierda derecha
for (int i = a.x; i < b.x; i++) {
int px = i;
int py = m * (px-a.x) + a.y;
SDL_RenderDrawPoint(renderer, px, py);
}
// de arriba a abajo
for (int i = a.y; i < b.y; i++) {
int py = i;
int px = (py-a.y) / m + a.x;
SDL_RenderDrawPoint(renderer, px, py);
}
SDL_RenderPresent(renderer);Con esto habremos aprendido a dibujar líneas rectas entre dos puntos en un espacio 2D. Estamos preparados para utilizar estas líneas conjuntamente con los vértices de nuestros modelos.
Creando nuestros primeros triángulos
Todo lo que tendremos que hacer es agrupar los vértices en triángulos. Tres vértices forman un triángulo y los lados de un triángulo se consigue dibujando 3 líneas rectas.
La buena noticia es que de este trabajo, suelen encargarse los programas de modelado en tres dimensiones. Si analizámos el contenido de un fichero OBJ de blender, podemos observar lo siguiente:
# Blender v2.76 (sub 0) OBJ File: ''
# www.blender.org
mtllib cubo.mtl
o Cube
v 1.000000 -1.000000 -1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 -1.000000 1.000000
v -1.000000 -1.000000 -1.000000
v 1.000000 1.000000 -0.999999
v 0.999999 1.000000 1.000001
v -1.000000 1.000000 1.000000
v -1.000000 1.000000 -1.000000
vn 0.000000 -1.000000 0.000000
vn 0.000000 1.000000 0.000000
vn 1.000000 0.000000 0.000000
vn -0.000000 0.000000 1.000000
vn -1.000000 -0.000000 -0.000000
vn 0.000000 0.000000 -1.000000
usemtl Material
s off
f 2//1 3//1 4//1
f 8//2 7//2 6//2
f 5//3 6//3 2//3
f 6//4 7//4 3//4
f 3//5 7//5 8//5
f 1//6 4//6 8//6
f 1//1 2//1 4//1
f 5//2 8//2 6//2
f 1//3 5//3 2//3
f 2//4 6//4 3//4
f 4//5 3//5 8//5
f 5//6 1//6 8//6Se observan dos bloques de datos. El primer bloque corresponde con la información de los vértices y el segundo el de las caras. Por ahora, diremos que una cara es, al uso, un triángulo. Las caras, vienen indicadas en un formato que por ahora, aporta información que no vamos a utilizar. Nos interesa extraer solo una parte:
Ejemplo: f 123//121 312//043 094//234 -> triángulo cuyos los vértices serían: 123, 321, 094Si imaginamos los vértices como un array, podemos utilizar estos valores como índices para acceder cada vértice. Con esto habremos solventado el problema de la creación de nuestros triangulos. Concretamente, en el ejemplo superior, tenemos 12 triángulos, 2 por cada cara del cubo, cada uno de ellos con sus tres vértices.
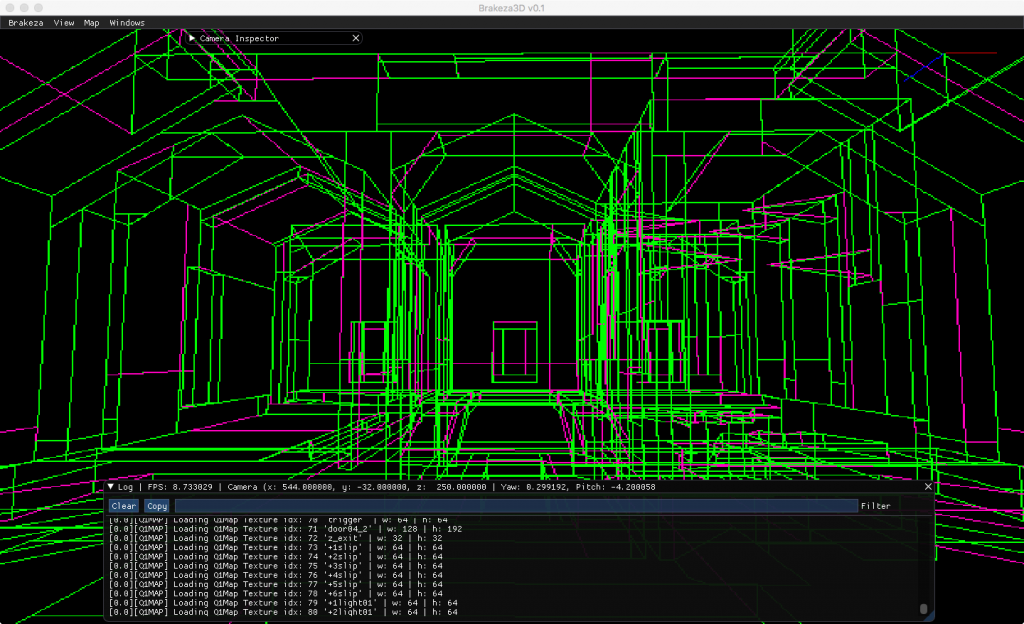
Con lo aprendido en artículos anteriores (Introducción a las 3D), podríamos convertir los 3 vértices de un triángulo a un espacio en dos dimensiones y al finalmente conectar estos puntos 2D mediante líneas rectas, consiguiendo el efecto de wireframe.
Si juntamos con línes los vértices de suzanne, obtendríamos el siguiente resultado:

Como siempre, podéis encontrar el código fuente del ejemplo en GitHub:
Resumen
Hemos aprendido a dibujar líneas rectas, lo que nos permite unir nuestros puntos en el plano 2D, para conseguir un motivador efecto de malla. Si estás interesado en un algoritmo optimizado para dibujar líneas, no dejes de ver el Algoritmo de Bresenham, una de las soluciones más recomendadas.





Deja una respuesta