Introducción a las 3D

Conceptos básicos

En el post anterior hemos visto como dibujar un pixel en una ventana mediante SDL. Un pixel por si solo, no impresiona demasiado, pero será suficiente para poder dibujar cualquier objeto 3D como veremos a continuación. Será nuestra introducción a las 3D.

Supongamos por ejemplo un cubo en tres dimensiones. Tiene 8 vértices, por tanto, sabemos que podemos pintar un cubo  dibujando 8 píxeles en pantalla (nos olvidamos por ahora de los lados del cubo). Hemos de ser capaces de calcular que posición ocupa cada pixel de ese cubo en nuestra pantalla bidimensional.

Cubo con 8 vértices

El primer problema que encontraremos será como saber llevar un punto del espacio 3D a un espacio 2D, como es nuestra pantalla.

Ejes de coordenadas

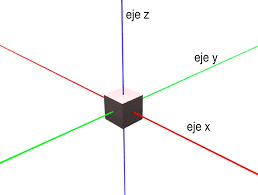
Como ya sabéis un punto en el espacio se define por sus componentes x, y, z respecto a un origen de coordenadas.

En su forma mas simple un objeto 3D estará formado por un conjunto de puntos donde cada uno ocupa una posición (x, y, z) en el espacio. Llamaremos vértice a un punto en el espacio y será nuestra primitiva 3D mas básica.

La Perspectiva

Recordad que podéis encontrar el código fuente en el repositorio.

Supongamos que disponemos de 8 vértices y su posición en el espacio:

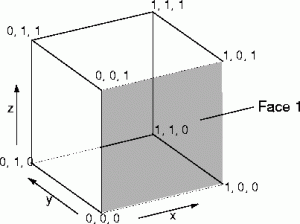
• v1(0, 1, 1)
• v2(1, 1, 1)
• v3(0, 0, 1)
• v4(1, 0, 1)
• v5(0, 1, 0)
• v6(1, 1, 0)
• v7(0, 0, 0)
• v8(1, 0, 0)

La forma de transportar un punto 3D en el espacio a un espacio 2D es dividir cada una de sus componentes horizontal y vertical entre su componente de profundidad, es decir, su z.

px = vx / vz;

py = vy / vz;

Esta división se encargará de prácticamente toda la magia, pero… ¿qué hace realmente?.  La palabra clave es la perspectiva.

En el mundo real cuanto mas lejos está un objeto mas pequeño lo vemos, en otras palabras, cuanta mas profundidad (z) tienen sus vértices, mas juntos los veremos en 2D, hasta juntarse en un punto (punto de fuga) en el que dejaremos de ver ese objeto. En definitiva observamos que nuestra fórmula hace que la posición 2D de cada vértice tienda a cero cuanto mayor es su profundidad en el espacio 3D.

Con este sencillo pero potente concepto, podemos lanzarnos a programar lo aprendido. Vamos a crear en nuestro código la información de los ocho vértices del ejemplo y a procesarlos para llevarlos del espacio 3D al espacio 2D y finalmente pintarlos en pantalla con lo aprendido en el post anterior.

Por ahora crearemos una simple estructura para almacenar la información de nuestros vértices con comodidad:

struct vertice {
    int x;
    int y;
    int z;
};

Inicializaremos un array con la información de cada vértice:

vertice v[7];
v[0].x = 0;  v[0].y = 1; v[0].z = 1;
v[1].x = 1;  v[1].y = 1; v[1].z = 1;
v[2].x = 0;  v[2].y = 0; v[2].z = 1;
v[3].x = 1;  v[3].y = 0; v[3].z = 1;
v[4].x = 0;  v[4].y = 1; v[4].z = 0;
v[5].x = 1;  v[5].y = 1; v[5].z = 0;
v[6].x = 0;  v[6].y = 0; v[6].z = 0;
v[7].x = 1;  v[7].y = 0; v[7].z = 0;

Y finalmente encapsularemos la división de perspectiva en una simple función por la que pasaremos cada vértice del cubo. Como particularidad y para diferenciar el cambio del espacio 3D al espacio 2D vamos a utilizar otro tipo de dato para almacenar la información de puntos en pantalla:

struct point2d {
    int x;
    int y;
};

point2d perspectiveDivision(vertice v)
{
    point2d p;
    p.x = v.x / v.z;
    p.y = v.y / v.z;

    return p;
}

Vemos que cuando un vértice pasa por la función perspectiveDivision obtenemos un punto en 2D listo para dibujar en pantalla.

Juntándolo todo

Si juntamos todas las piezas veremos algo similar a la siguiente captura:

Tenemos cuatro vértices. ¿Dónde están los cuatro que faltan?. Es correcto por ahora ya que estamos viendo el cubo de forma perpendicular a la cámara  y no vemos los 4 vértices que están detrás de los que si vemos, sencillamente están perfectamente alineados.

Por ahora y al no haber implementado nada mas específico, nuestra “cámara” se encuentra así por defecto: en la posición (0, 0, 0) mirando al frente (hacia z). En futuros posts hablaremos de la cámara y su manipulación, una parte fundamental del engine.

Veámos otro ejemplo con el mismo código pero aportando los vértices de otro modelo 3D. Concretamente vamos a utilizar 1448 vértices que conforman la cabeza de la mona Suzanne. Podemos ver el resultado:

Cabeza de Suzanne (desde arriba)

Podéis descargar el código fuente completo en:

Watch

Resumen

El objetivo de este post es introducir el concepto de la perspectiva y ofrecer un mecanismo sencillo para transportar vértices en tres dimensiones a puntos bidimensionales que poder representar en pantalla mediante píxeles.

Nuestro engine ahora es capaz de representar los píxeles de un modelo 3D en pantalla. De momento no podemos hacer nada mas. En futuros post ampliaremos esta información profundizando en el concepto de cámara.

En el siguiente post aprenderemos a rotar, mover y escalar nuestros modelos 3D.