Buenas a tod@s de nuevo! Tras unos meses liado con un cambio de curro volvemos a la carga con un tema de obligado tratamiento en cualquier motor 3D: Las colisiones.

Cabe destacar que existen diferentes aproximaciones a este problema: Por un lado existen librerías de renombre que nos ofrecen un sistema completo de colisiones además de físicas realistas. En esta liga podemos mencionar Havok, Physx de Nvidia o como alternativas OpenSource Bullet u ODE, todas ellas bastante buenas.

Es normal que surjan dudas del tipo: ¿Qué librería adoptar?, ¿las alternativas OpenSource son competitivas?, ¿Necesita mi gameplay un sistema de físicas realistas?…

Es importante centrarse en el gameplay que deseamos implementar y analizar a fondo las características que ofrece cada librería, me explico: Todas son librerías muy buenas en cuanto a su tratamiento en físicas, incluidas las gratuitas, pero no todas están orientadas al mundo del videojuego, lo que puede hacer que esa fase de implementación del gameplay a medida, pueda hacerse cuesta arriba.

En mi experiencia con Bullet, aunque conseguí implementar un gameplay a través de su “CharacterController” y hacerlo funcionar con éxito, el mismo Erwin Coumans (Brain Team de Google y main dev de la librería), menciona que esa implementación está deprecated, sin ir más lejos, la demo está fuera de la rama master en GitHub, tiene bastantes fallos.

¿Por dónde empezar?

Lo más probable es que el gameplay que hayas ideado, no requiera por si mismo la integración de un sistema de físicas realistas, las cuales, como podéis imaginar tienen su complejidad de implementación, pero que además impacta en el rendimiento general de la aplicación. 

Suele ser suficiente con implementar un sencillo sistema de colisiones basado en primitivas básicas que someteremos nuestro antojo y posiblemente a las leyes de Newton.

En la práctica, es muy habitual que un motor 3D implemente su propio sistema de colisiones para soportar su gameplay y por otro lado añada una integración con una librería de físicas para interacción de elementos del escenario o fases scriptadas del juego.

Por mencionar algunas referencias: Quake y/o Mario Bros, no utilizan un sistema de físicas realistas, sin embargo el gameplay genera colisiones y es reactivo a ellas. Por otro lado tendríamos a Half-Life 2, en el que puedes lanzar un bidón por los aires y verlo caer con físicas realistas golpeando el escenario, es un claro ejemplo de sistema mixto, por un lado el gameplay está basado en colisiones sencillas (es de hecho el mismo que el Quake) y por otro lado algunos de los elementos del entorno están sometidos a Havok y reaccionan con físicas realistas.

En la práctica, es muy habitual que un motor 3D implemente su propio sistema de colisiones para soportar su gameplay y por otro lado añada una integración con una librería de físicas para interacción de elementos del escenario o fases scriptadas del juego.

Por lo dicho, en Brakeza3D he optado por un enfoque mixto con un gameplay implementado por mi mismo y en otra capa, ofrezco la posibilidad de integrar estos objetos 3D con un sistema de físicas realistas a través de Bullet. Así que con este enfoque continuamos!

Lo básico

El primer reto a la hora de implementar un sistema de colisiones es elegir las primitivas 3D con las que deseas trabajar: las habituales son la esfera y el cubo, además de sus versiones no simétricas las elipsoides y paralelepípedos rectangulares.

Imaginad vuestro mundo 3D como una serie de formas primitivas, donde un humano se convertirá en un elipsoide, una casa en un cubo o un planeta en una esfera y así sucesivamente:

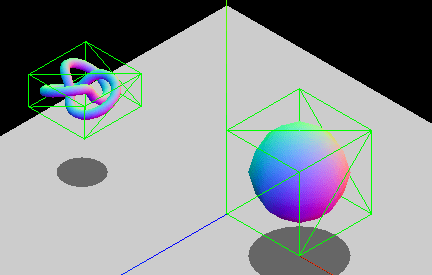
En una primera instancia debemos de ser capaces de detectar cuando una de estas primitivas está interseccionando con otra.

Una esfera viene determinada por su posición y su radio, cualquier objeto a una medida igual o menor a ese radio, estará en contacto con la esfera.

Ejemplo colisión “sphere vs plane”:

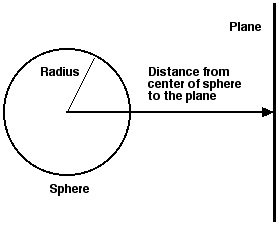
Ejemplo de colisión “sphere vs sphere”:

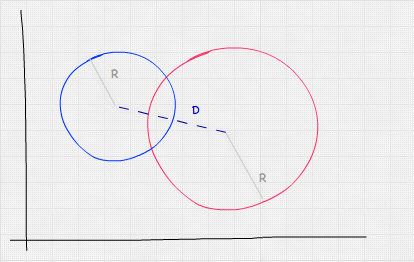
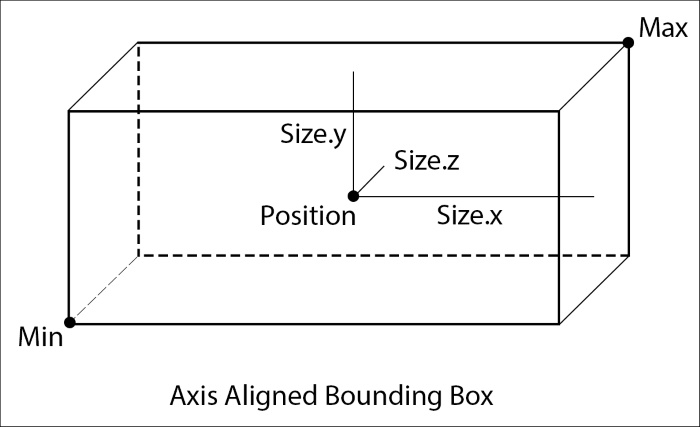
A los paralelepípedos que usaremos en las colisiones los llamaremos “Bounding Box” y vienen determinados por su posición y su vector de mínimos y máximos. En la siguiente imagen podéis ver el análisis de colisión de un AABB vs AABB en el eje X. Apenas con unas restas podemos resolverlo. Sería cuestión de replicar este test en los ejes Y y Z para completar el test y ya estaría.

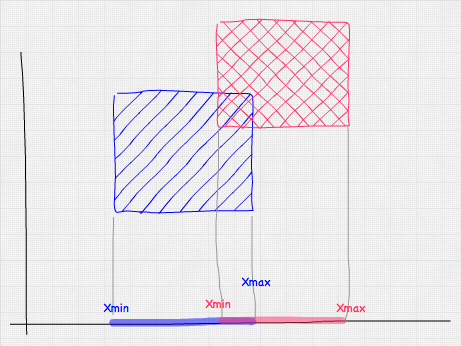
La implementación de estas dos primitivas es tan sencilla que no profundizaremos en ellas.

Bounding Boxes Alineados (AABB)

Una simplificación habitual a la hora de implementar un sistema de colisiones basado en Bouding Boxes consisten en no rotar nunca los Bouding Boxes, es decir, las cajas que representan los objetos no rotan respecto al mundo real, aunque si lo haga el objeto que representa. Imaginemos un enemigo, es libre de rotar sobre si mismo, pero esa rotación no será tenida en cuenta para el sistema de colisiones.

Es habitual disponer de un sistema de colisiones AABB como sistema temprano de detección (lo encontraréis referido como broadphase collision), que en caso de desencadenar una colisión da paso a un sistema más preciso de respuesta, que por ejemplo pueda responder si le hemos colisionado por la espalda o bajo alguna circunstancia específica.

Detección continua de colisiones

En este punto, estaríamos en disposición de implementar un sistema de colisiones que detectase intersecciones de forma estática, es decir, podemos preguntarle al motor si dos elementos interseccionan y éste nos responderá booleanamente.

Esto está genial y es un gran avance, pero por si solo puede esconder algunas deficiencias. Pensemos en el framerate y la velocidad: El framerate viene a determinarnos el número de veces máximo que podemos detectar colisiones en cada frame. Se convierte en un límite insuperable. ¿Y qué pasa con la velocidad? Pues la velocidad de un objeto en nuestro motor 3D, tampoco escapa a los límites del framerate. Veamos la siguiente imagen:

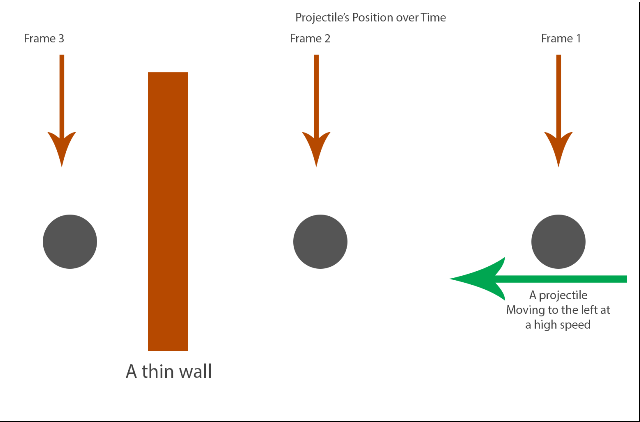
En caso de que la velocidad supere con creces los límites del framerate el sistema fallará. Imaginad una pared sobre la que disparáis una bala, en el frame 0 la bala apenas estará saliendo de la pistola del personaje, pero por su altísima velocidad, en el frame 1 ya se encontraría muy lejos de la pared con la que debería haber chocado. En este escenario, las comprobaciones estáticas de colisiones, no resuelven el problema, ya que el sistema nos indicaría que no se produce la colisión en ningún frame.

Es por este motivo que existe el concepto de Detección Continua, el cual se encarga de responder no solo a la pregunta de si dos elementos interseccionan, sino que además nos ofrece información adicional de cuando y donde se producirá una colisión para poder reaccionar a ello. Además es una solución independiente del framerate resultante.

La detección continua está ligada al concepto de traza. Una traza será el resultado de preguntarle al sistema de colisiones si un elemento colisiona con otro. Principalmente el resultado de una traza consiste en el valor devuelto entre el rango [0-1], donde un 0 supondría una colisión inmediata, donde no es posible el movimiento y donde un 1 supondría el éxito al realizar un movimiento completo, es decir, donde podríamos aplicar todo el vector velocidad solicitada al cuerpo en movimiento. En definitiva el rango de la traza determinará la escala que podemos usar de la velocidad solicitada.

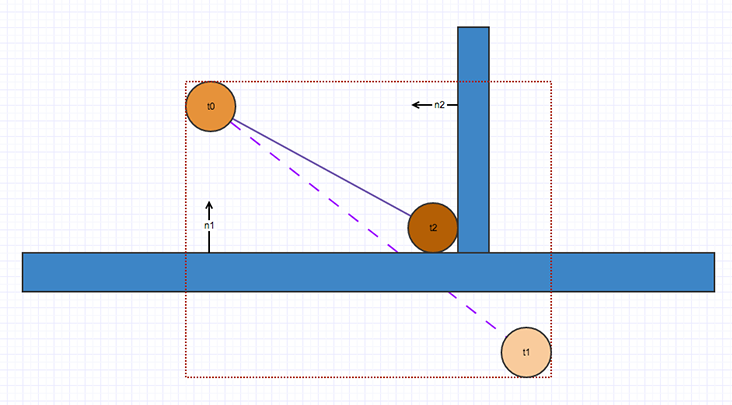
Deslizamientos

Una vez disponemos de un sistema de colisiones continua basado en trazas, el siguiente obstáculo consiste en resolver cómo vamos a satisfacer las colisiones cuando éstas se produzcan para ofrecer una experiencia de gameplay satisfactoria. Me estoy refiriendo al movimiento del personaje principal a través del escenario. Esto implica poder subir peldaños, chocar con una pared o deslizarse a una velocidad acorde al ángulo de golpeo. En definitiva un conjunto de situaciones que constriñen las posibilidades de movimiento en función del escenario.

Supongamos que el personaje choca con una pared, el movimiento en el plano que representa la pared queda constreñido a la misma, en caso de que el movimiento choque con dos paredes, es decir, una esquina, el movimiento quedará constreñido a los dos planos que representan esas paredes, lo mismo sucede si el movimiento está limitado por tres planos, hasta alcanzar un máximo de cuatro planos, en los que ya no sería posible realizar ningún movimiento.

La técnica que resuelve todos estos problemas, es la misma: Los deslizamientos.

El deslizamiento aplica de igual forma en vertical que en horizontal, es arbitrario, por tanto resolveremos de igual forma las colisiones con paredes verticales, que contra irregularidades en el suelo.

Una vez detectada una colisión contra un plano en base a un vector de velocidad dado, proyectaremos la velocidad sobre el plano de colisión y generaremos un nuevo vector velocidad paralelo al plano de golpeo cuyo tamaño dependerá de la proyección mencionada. Veamos un ejemplo:

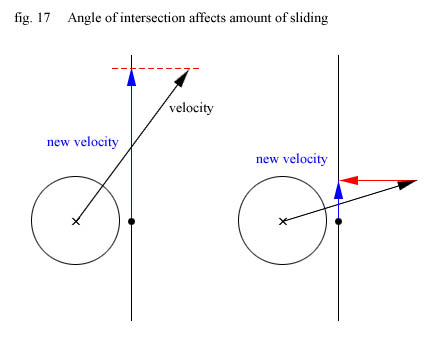
Esto lo haremos por cada plano en el que hayamos detectado una colisión, hasta que nos encontremos con un máximo de cuatro planos, situación que no debería producirse, ya que nos quedaríamos “clavados”.

Gravedad

Esta suele ser la parte más sencilla: Antes de la fase de deslizamiento descrita arriba,  añadiremos en cada frame la aceleración correspondiente a la gravedad a nuestra velocidad. Básicamente disponemos de una velocidad inicial, a la que sumaremos la velocidad del frame correspondiente.

Para ello simplemente debemos disponer del deltaTime de cada frame, es decir, el tiempo que tarda el engine en generar cada frame.

Clavadas

Bueno a pesar de toda la teoría que podáis encontrar, no hay ningún sistema de colisiones que no disponga de un sistema “anti-stuck”, es decir, un sistema que se encarga de monitorizar constantemente que no estás clavado (el número de planos máximos de colisión es menor a 4).

La realidad es que estas situaciones suceden, en ocasiones debido a imprecisiones de cálculo intrínsecas al tipo de dato elegido.

Un sistema de anti-stuck básico, almacena la última posición en la que no se produjo ningún error grave en el sistema de colisiones y ante un posible escenario de bloqueo, nos lleva a dicha posición. No dejan de ser parches ante situaciones que no deberían estar ahí, pero están. Mucho ojo con esto, ya que podéis perder días revisando cálculos y estar correctamente!

Código fuente

He aglutinado todo el código relativo a las colisiones en un único fichero. En mi caso implementé por mi mismo un sistema de colisiones basándome en una esfera contra una sopa de triángulos (el mapa), aunque finalmente lo descarté y opté por utilizar exactamente el mismo sistema que Quake (AABBs), literalmente extraje el código y lo adapté a Brakeza3D, no sin sufrimiento tengo que decir. El código de colisiones del Quake es una pesadilla, por mucho que idolatre a Carmack :P.

Como única particularidad a lo ya dicho, el Quake (Id Tech1), dispone por cada modelo (o brush), unos planos de corte, que son sobre los que nos apoyaríamos para realizar los test de colisiones. Estos planos determinarán nuestro AABB de colisión.

Concretamente cada modelo del Quake tiene tres conjuntos de planos de corte, cada uno con menor nivel de detalle, los que usaremos a modo de LOD de la colisión. Si nos encontramos muy cerca de un objeto, usaremos su set de planos de corte de mayor detalle, a medida que nos alejemos de tal objeto, pasaremos a usar conjuntos de planos de corte de menor detalle.

Podéis ver el código aquí:

https://github.com/rzeronte/brakeza3d/blob/master/src/Physics/BSPCollider.cpp

Resumen

Nos hemos aproximado a la solución de las colisiones en un entorno 3D, presentado las primitivas básicas de colisión y las diferencias existentes entre un sistema de colisión continua y uno que no lo es. Además hemos atendido al tratamiento de la respuesta de colisiones a través de un sistema de deslizamiento.

Las técnicas descritas en este documento siguen muy vigentes hoy en día y pueden aplicarse perfectamente al mundo de las 2D. Volveremos en próximos artículos avanzando sobre la integración de físicas realistas sobre Bullet Physics. Un saludo!