Inteligencia Artificial en 3D

Buenas a todos! En mi último artículo os hablé sobre el Z-Buffer y el tipo de problemática que solventa. En esta ocasión, voy a dejar de lado el render como pieza de software y vamos a hablar de cómo podríamos aproximarnos a la Inteligencia Artificial en 3D.
Si estáis implementando vuestro propio motor 3D, es para probablemente, hacer un videojuego o alguna pieza de software susceptible de requerir Inteligencia Artificial en 3D.
En mi opinión el “Hola mundo” de la IA en videojuegos, consiste en poder mover objetos de un punto A a un punto B, detectando los posibles obstáculos que haya por en medio y actuar en consecuencia. Habréis visto este comportamiento en cualquier juego, del tipo que sea, cuando un NPC os ataca, u os persigue, etc.
El algoritmo de pathfinding más común es: A* (A-Star). Podéis encontrar un análisis sobre diferentes algoritmos de pathfinding en este estupendo PDF. Existen en Internet multitud de páginas que documentan este algoritmo, pero la gran mayoría, explican el problema desde el punto de vista de juegos 2D. Y es que el es relativamente sencillo entender el algoritmo A* en 2D. Los más familiarizados con la teoría de autómatas (grafos/digrafos), no tendréis problemas en asimilarlo. Al fin y al cabo dispondréis de un grafo y se trata de calcular el camino más corto.
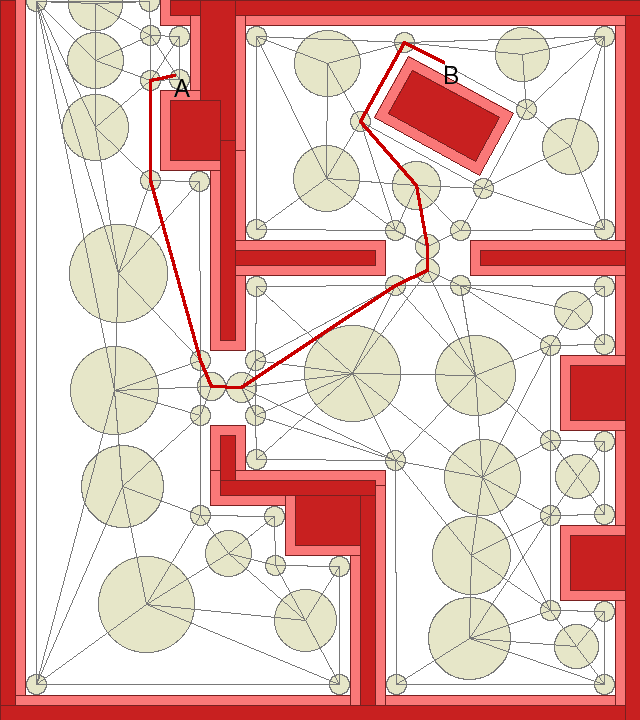
Dicho esto, lo habitual con una escena 2D es trocearla en “cuadrículas” o “hexágonos”, las cuales convertiremos en “vértices” de nuestro grafo para finalmente calcular el camino, si existe. Os podéis hacer una idea observando la siguiente imagen:
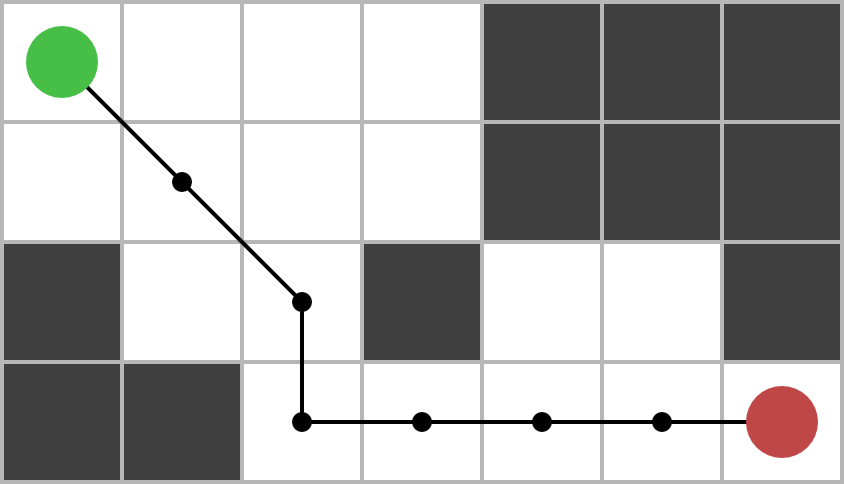
En un juego 2D, una vez disponéis de la capacidad de pathfinding de vuestros elementos, ya podéis implementar una máquina de estados que determine el comportamiento a seguir en cada caso: perseguir, ataca, buscar munición, huir hacia…
El problema viene a la hora de visualizar como aplicar el algoritmo A* en 3D, donde el mapeo de nuestro grafo, se complica.
Grafo en 3D
En nuestro motor 3D, tan solo disponemos de geometría, es decir, una sopa de triángulos que conforman una escena. La cosa se complica, si tenemos en cuenta que en un mundo 3D hay escaleras, pendientes, esquinas, puentes y/o puertas que pueden impedir la creación de un camino entre dos puntos. Todo esto, ha de ser tenido en cuenta a la hora de crear nuestro grafo.
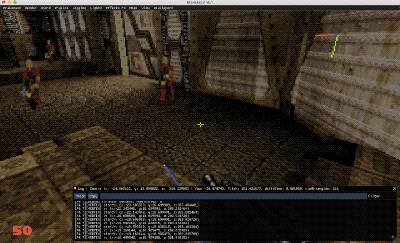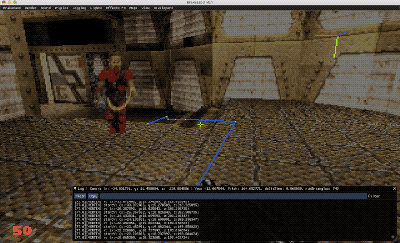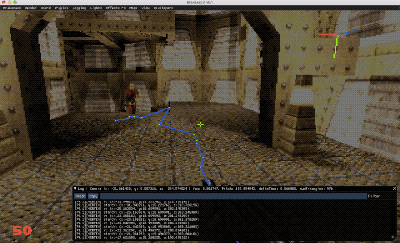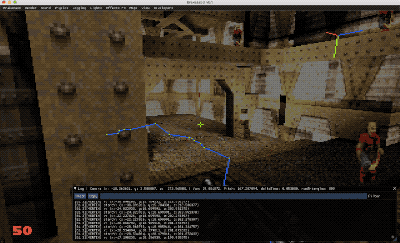
En el GIF superior extraído directamente de Brakeza3D, podéis ver como se genera un camino entre un punto A y la posición del jugador en movimiento en tiempo real. Observar como el pathfinding va sorteando escaleras y doblando esquinas.
El algoritmo A* es n-dimensionable, no está limitado a su aplicación en 2D, simplemente hemos de crear un grafo correctamente por el que poder saltar entre vértices.
Malla de navegación
Su nombre es bastante acertado, se trata de un subconjunto de la geometría de vuestro escena al completo, sobre la cual podemos desplazarnos, según nuestros requisitos. En la siguiente imagen podéis ver de color azul, un ejemplo de malla de navegación:

Supongamos que hablamos de un juego con gravedad, de tipo First Person Shooter ¿Cuál sería la malla de navegación del mapa?. Al menos, podemos garantizar que toda la geometría relativa al suelo: por la cual los personajes podrán moverse.
Hemos por tanto de diseñar un sistema, capaz de articular un grafo basándose en nuestra malla de navegación, la cual hemos de calcular previamente. Cómo os podéis imaginar, esto no será barato en términos de ciclos de CPU, por tanto conviene pre-cachear las mallas de navegación de la escena que vayamos a usar, antes de utilizarla, por ejemplo en tiempo de carga.
Cómo calcular la malla de navegación?
Lo cierto, es que no es nada trivial: Vayamos por pasos. Las mallas de navegación varían en función de los requisitos que les pidamos a estas.
Una malla de navegación que se precie, dispone de multitud de parámetros a la hora de configurarse. Por mencionar los más obvios, de ejemplo:
- Inclinación máxima aceptada
- Altura de paso máxima
- Margen contra paredes
Ya hemos dicho que nuestro mapa puede tener escaleras y/o puentes, los cuales tendrán peldaños “perpendiculares” al suelo y aun así hemos de aceptar como válidos, mientras el escalón sea “superable” por nuestros personajes (altura de paso máxima). De forma similar los puentes pueden estar inclinados (inclinación máxima) y también deben ser superables por nuestra IA.
La configuración de la malla de navegación puede ser tan compleja según vuestros requisitos.
En una segunda instancia, habrá que tener en cuenta geometría de nuestro mapa la cual no es accesible por nuestros personajes, aunque cumpla estos requisitos, por ejemplo, si estamos implementando un FPS y diseñamos geometría dedicada a “agua/lava” donde no queremos que nuestros NPCs caminen, habremos de preocuparnos de descartar dicha geometría en la creación de la malla de navegación, suena obvio.
Cálculo de la malla de navegación
Voy a desarrollar la versión más simple de una malla de navegación: Nuestro objetivo será recorrer toda la geometría, es decir, recorreremos triángulo a triángulo la escena y por ahora, nos limitaremos a comprobar la inclinación del triángulo respecto al vector UP (la vertical, (0, 1, 0)). Para ello será necesario disponer de la normal del triángulo, ya hemos hablado de ello en otros artículos. Hallaremos el ángulo entre ambos vectores, si el ángulo se encuentra dentro de nuestros requisitos añadiremos dicho triángulo a nuestra malla de navegación.
Podéis encontrar ver el siguiente video para aprender a calcular el ángulo entre dos vectores.
En una segunda instancia, con los triángulos que hemos preseleccionado, construiremos nuestro grafo. Recorreremos cada triángulo y calcularemos los triángulos conexos a este, es decir a los que habría un posible camino. Así recursivamente construiremos nuestro grafo.
Resuelto esto, ya dispondríamos de un grafo “manejable” que representa los caminos posibles a través de nuestra malla de navegación, y sobre la que podríamos ejecutar un Pathfinding.
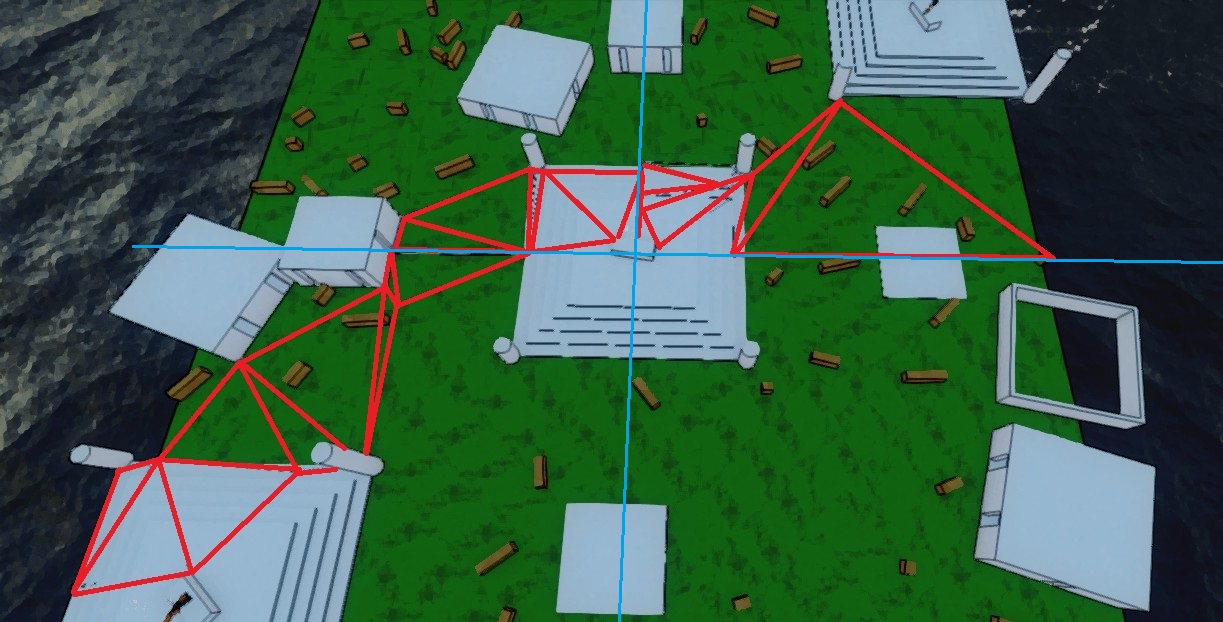
Si observáis la imagen inferior, podéis ver el desarrollo de un pathfinding entre dos puntos en una geometría 3D. Se ve la clara relación entre los triángulos y los vértices del grafo
Librerías de terceros
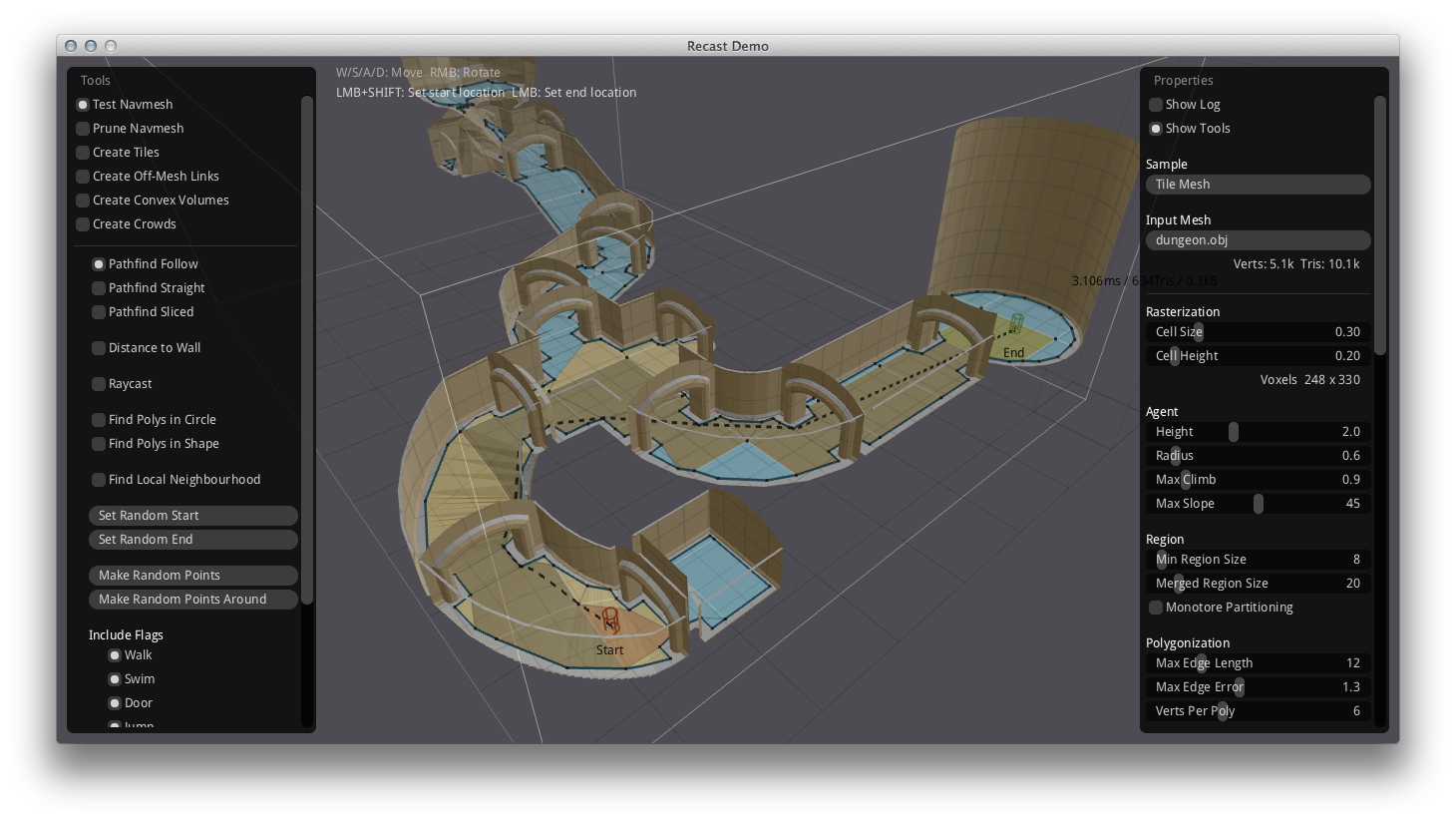
Si implementar por vosotros mismos lo descrito arriba os resulta demasiado laborioso, siempre podéis optar por la adopción de alguna librería de terceros que os resuelva el problema. Os recomiendo: Recast Navigation.
Recast Navigation os permitirá una gran flexibilidad a la hora de configurar vuestras mallas de navegación. Además ofrece algunos extras a la hora de calcular pathfindings, raycast, parábolas y multitud herramientas que serán muy útiles a la hora de interpretar la geometría de un mapa en un videojuego.
Resumen
Hemos aprendido un método para aproximarnos a la Inteligencia Artificial en 3D. Con este método, podremos ser capaces de implementar algoritmos de pathfinding que nos abrirán la puerta a desarrollar sistemas de Inteligencia Artificial en 3D aún más complejos.

