Buenas a todos nuevamente!. En el artículo anterior descubrimos las bases en las que se apoya el sistema de iluminación de un engine 3D. Hoy me gustaría hablar de algo que hemos pasado por alto hasta ahora: La importancia del winding order y el back-face culling.
Realmente es un concepto muy sencillo: El órden de los vértices en el que conformes los vectores que representan los lados de tu triángulo IMPORTA.
Sin entrar todavía en las matemáticas que subyacen, seguro que todos hemos visto alguna vez un modelo 3D con «pelitos» de esta guisa:

Cada uno de estos «pelitos» es el vector normal de un triángulo del modelo. Y como bien sabréis un vector normal es aquel perpendicular a una superficie, por tanto cada «pelito» será un vector perpendicular hacia la cara del triángulo.
El detalle que vamos a enfatizar hoy es la dirección de la normal. Si observamos la imagen superior vemos que cada «pelito» surge hacia afuera de la tetera. Y es que no podemos olvidar que un triángulo en el espacio tiene DOS CARAS. Pues nuestro querido pelito identifica una de esas caras respecto a la otra.
¿Y todo esto a cuento de qué?
Ya sabes que un triángulo está formado por tres vértices ABC, que conforman los tres lados del mismo. Con esta información calculamos la normal del triángulo.
El problema en el fondo es que no es lo mismo formar el triángulo con los vectores AB, BC y CA, que usar, por ejemplo, BA, BC, AC. Y es que el producto vectorial o cross product entre vectores se ve afectado por este cambio, asi que debemos respetar SIEMPRE el orden de enrollamiento de los triángulos en nuestro motor.
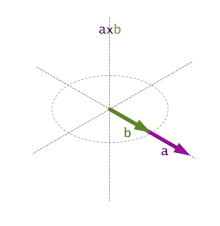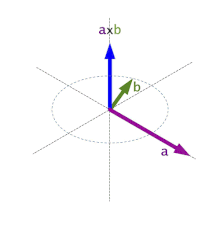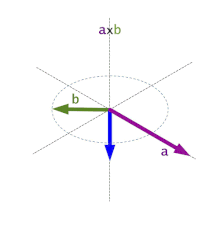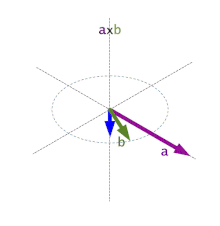
En la imagen superior podéis observar cómo varia el vector resultante del producto vectorial entre dos vectores, de ahí la importancia de respectar el enrollamiento o winding de todos los vértices, ya que no deseamos que un «pelito» salga en la dirección equivocada. Si nuestros cálculos no son consistentes con el enrollamiento, obtendremos resultados inestables según qué técnica estemos implementando.
Supongamos AB x BC y BA x CB, os invito a realizar los cálculos, comprobaréis que la normal resultante varia.
Convenios existentes
En la práctica, cualquier editor 3D exporta la geometría respetando un orden de enrollamiento adecuado, acorde a uno de los dos siguientes esquemas:
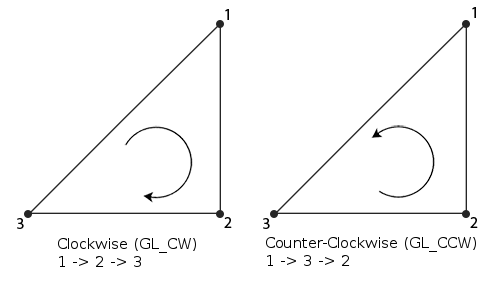 Una vez que podemos garantizar que toda nuestra geometría respeta un winding order, estaríamos preparados para implementar cualquier técnica que se apoye en las normales de los triángulos, que no son pocas.
Una vez que podemos garantizar que toda nuestra geometría respeta un winding order, estaríamos preparados para implementar cualquier técnica que se apoye en las normales de los triángulos, que no son pocas.
Back-Face Culling
Una de las features básicas de cualquier engine3D es la de la ocultación de las caras ocultas (HSR). Esta técnica se apoya en la normal del triángulo para determinar si un triángulo es visible o no desde un determinado ángulo de visión (como nuestra cámara).
El back-face culling se apoya en el el uso del «dot product» o producto punto, el cual nos devuelve un número, no un vector. Para esta técnica, el resultado de dicha operación no nos importa tanto como el SIGNO de la misma.
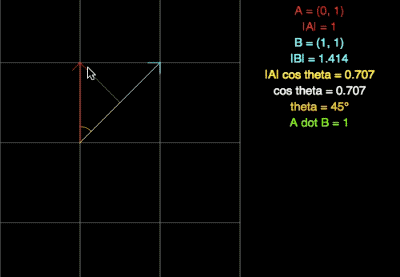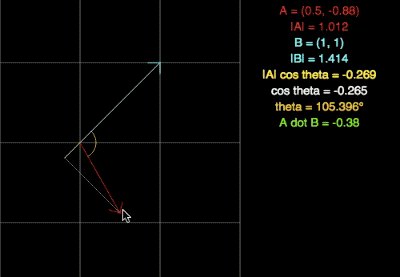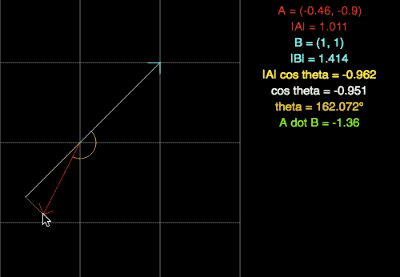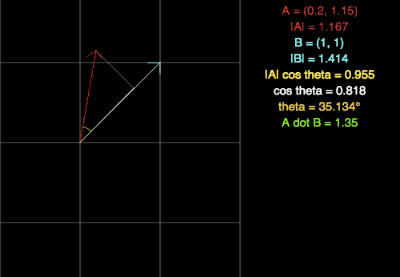
Podéis probarlo vosotros mismos en este link: https://www.falstad.com/dotproduct/
Veámos a continuación el código que realiza el back-face culling en Brakeza3D:
// * == dot product
bool Triangle::isBackFaceCulling(Vertex3D *position)
{
// Camera-triangle vector
Vertex3D v = this->Ao - *position;
return (v * this->getNormal()) >= 0;
}
Con esta sencilla técnica podremos descartar el rasterizado de triángulos, ya que no serán visibles. Es una técnica muy básica pero que reduce drásticamente el trabajo del render.
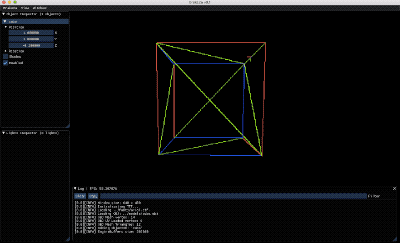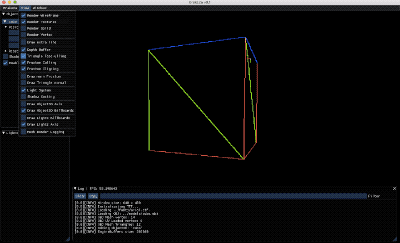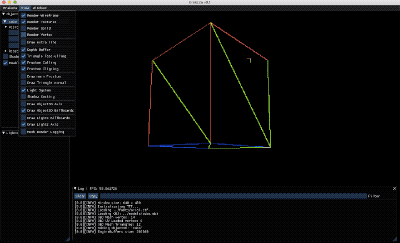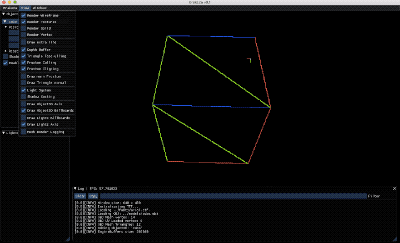
En la imagen superior podéis ver el back-face culling aplicado a los12 triángulos de un cubo (el gif activa y desactiva el backface culling)
Resumen
Hemos presentado la importancia de respetar el winding order con los vértices de un triángulo y un ejemplo de back-face culling, técnica que se vería afectada por una mala gestión del winding order. Esta técnica además es de obligada implementación, ya que reduce drásticamente el número de triángulos involucrado en una escena.





Deja una respuesta