Movimiento y rotación en el espacio 3D
En el capítulo anterior hemos visto como transformar vértices en el espacio en tres dimensiones hacia un plano en dos dimensiones como es nuestra pantalla sobre la que podemos pintar píxeles. En otras palabras, con lo visto hasta ahora podríamos cargar la geometría de un objeto y visualizarla como píxeles inconexos en pantalla. Todo ello de forma estática, sin vida, ni movimiento.
Antes de profundizar en este campo cabe destacar que existen diferentes aproximaciones para implementar el movimiento y rotación a vértices en el espacio. Es muy común encontrar información relativa a matrices y quaterniones como mecanismos que resuelven el problema. Por ahora evitaremos estos caminos para afrontar el problema desde un punto de vista mas simplista, aunque en algún momento adoptaremos estos mecanismos por sus múltiples ventajas.
Posición de un objeto en el espacio
Ya hemos visto que un vértice en el espacio está definido por sus tres componentes (x, y, z) respecto a un origen de coordenadas (habitualmente denominado por la letra O).
Mover un vértice en el espacio no es una tarea demasiado exigente. Si conocemos sus componentes horizontal (x), vertical (y) y de profundidad (z), para moverlo necesitamos alterar cualquiera de estas componentes según nuestras necesidades. Lo habitual será sumar y restar la cantidad deseada de movimiento en cada componente. Este mecanismo es conocido como translación (translation).
Si recuperamos el código fuente del post anterior, podemos jugar con las componentes de los vértices de Suzanne para observar su comportamiento. Para ello añadiremos una sencilla función a nuestro ejemplo, que alterará la posición de cada vértice:
vertice mueveVertice(vertice v, float x, float y, float z)
{
vertice vt;
vt.x = v.x + x;
vt.y = v.y + y;
vt.z = v.z + z;
return vt;
}Ahora utilizamos esta función para mover todos los vértices de Suzanne antes de aplicar la división de perspectiva. En este ejemplo aplicamos un movimiento de (1, 1, 3) respecto a la posición actual del vértice. Veamos el código:
for (int i = 0; i<=1448; i++) {
v[i] = mueveVertice(v[i], 1, 1, 3);
point2d p = perspectiveDivision(v[i]);
SDL_RenderDrawPoint(renderer, p.x, p.y);
}
Veámos la diferencia entre el resultado antes y depués de aplicar nuestra función de movimiento a cada pixel:
Antes de mover los vértices
Después de mover los vértices
Se puede apreciar como los vértices se mueven y que lo hacen con cierta homogeneidad, un resultado aceptable por ahora.
Si capturamos con los cursores del teclado y modificamos las componentes de los vértices, tendríamos nuestro primer modelo3D con movimiento controlado por nosotros, sería un gran avance que os invito a implementar por vosotros mismos.
Rotación de un objeto 3D en el espacio
La rotación de un objeto 3D en el espacio supone la rotación individual de cada vértice que lo forma. La solución está en la trigonometría.
Mantengamos la calma, todavía no es el momento de salir corriendo con las manos levantadas. Nos encontramos ante uno de esos conceptos que es de vital importancia comprender para implementar nuestro motor 3D, pero que en la práctica se reduce a un copy-paste de fórmulas copiadas de la wikipedia. Lo importante para nosotros será entender los rudimentos de como se rota un objeto en el espacio y sobre todo tener la capacidad de imaginar este movimiento en nuestra cabeza.
Finalmente será inevitable acudir a las matemáticas para que hagan el trabajo sucio.
 Para rotar un vértice en tres dimensiones, antes hemos de ser capaces de rotar un punto en dos dimensiones.
Para rotar un vértice en tres dimensiones, antes hemos de ser capaces de rotar un punto en dos dimensiones.
Conviene destacar que una rotación siempre es una operación referida a un punto, es decir, cuando rotamos un objeto, lo hacemos respecto de algún otro punto en el espacio, en nuestro caso rotaremos respecto al origen de coordenadas.
Las rotaciones se indican en grados o en radianes. Generalmente será mas fácil pensar en grados para imaginar las rotaciones, pero las operaciones matemáticas necesitan radianes para obtener resultados correctos. Por tanto será de gran utilidad un mecanismo para convertir las rotaciones de una escala a otra.
La rotación máxima en grados es 360º y 2PI en radianes, superados estos valores en cada escala, habremos dado una vuelta completa y nos encontraremos en nuestro punto de origen.
La fórmula que nos permitirá rotar un punto (x1, y2) un ángulo determinado es:
x2 = x1 * cos(angulo) - y1 * sin(angulo)
y2 = x1 * sin(angulo) - y1 * cos(angulo)Pero ¿De donde sale esta fórmula?.
Supongamos que tenemos un plano 2d con un punto que deseamos rotar respecto al origen. Además vamos a imaginarnos un círculo cuya circunferencia pasa por nuestro vértice y que además tiene el centro en el origen de coordenadas.
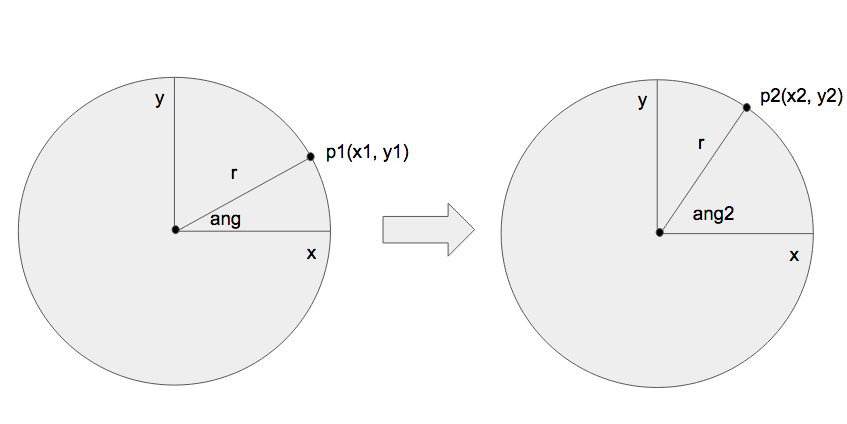
El radio de este círculo será la distancia entre el origen y nuestro punto. Además podemos observar que su distancia no variará una vez rotado. Como si girasemos una cuerda con una bola atada al final del extremo con nuestra mano, el tamaño de esta cuerda no variaría en el giro.
La distancia entre dos puntos (o el módulo de un vector entre dos puntos) viene determinado por la siguiente fórmula:
distancia = raiz_cuadrada( (x2-x1)^2 + (y2-y1)^2 );Una vez que sabemos la distancia entre estos dos puntos (recordemos que es el radio de la circunferencia) haremos uso de la trigonometría para resolver las coordenadas finales de nuestro punto rotado. Para ello necesitamos utilizar los senos y los consenos. Estos no son mas que una relación entre los tres lados de un triángulo, que recordamos que tienen dos catetos adyacentes y una hipotenusa. Esta relación es la siguiente:
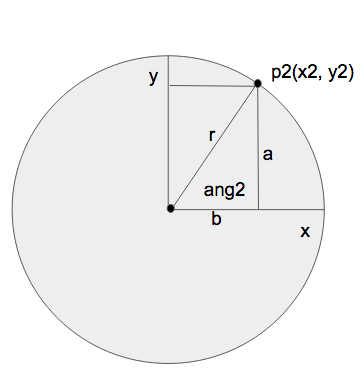
sin(θ) = Opuesto / Hipotenusa cos(θ) = Adyacente / Hipotenusa
De los tres lados del tríangulo formado en nuestra nueva rotación ya sabemos el valor de r, nos falta averiguar a y b para obtener las coordendas de x2 y y2. Lo que si sabemos es el valor del ángulo que vamos a rotar. Nos apoyaremos en las fórmulas del seno y conseno para obtener a y b.
Podemos observar como r es la hipotenusa y que a y b son los catetos. Si sustituimos en la fórmula del seno:
sin(θ) = a / r;
A continuación podemos despejar el valor de a:
a = sin(θ) * r
Una vez conocemos a y r, solo nos queda por averiguar b. Si sustituimos en la fórmula del coseno:
cos(θ) = b / r;A continuación podemos despejar el valor de b:
b = cos(θ) * r;Con esto ya tenemos el valor de los tres lados del triángulo. Hemos terminado!.
Ejemplo de rotación de un punto en un espacio 2d
Recordad que las funciones de seno y coseno esperan radianes para trabajar, por lo que si deseamos utilizar grados vamos a ncesitar convertirlos previamente. Podemos convertir grados a radiantes con la siguiente función:
float degreesToRadians(float angle)
{
return angle * (float) M_PI / (float) 180.0;;
}Utilizando el desarrollo visto arriba, vamos a crear nuestra función que rota un punto respecto a otro:
point2d rotaVertice(point2d o, point2d p, float angulo)
{
float r = sqrtf( powf( (p.x-o.x), 2) + powf( (p.y-o.y), 2) );
float a = sinf(degreesToRadians(angulo)) * r;
float b = cosf(degreesToRadians(angulo)) * r;
point2d p2;
p2.x = b + o.x;
p2.y = a + o.y;
return p2;
}Ahora utilizarmos esta función a para rotar un punto 360 grados, para lo cual iteraremos 360 veces donde rotaremos cada vez un grado de mas nuestro punto. El código sería el siguiente:
point2d center;
center.x = WINDOW_WIDTH/2;
center.y = WINDOW_HEIGHT/2;
point2d p;
p.x = (WINDOW_WIDTH/2) + 100;
p.y = (WINDOW_HEIGHT/2) + 100;
for (int i = 0; i<=360; i++) {
point2d rotated_point = rotaVertice(center, p, (float) i);
SDL_RenderDrawPoint(renderer, rotated_point.x, rotated_point.y);
}
SDL_RenderPresent(renderer);Cuyo resultado como se puede apreciar es una circunferencia perfecta:
![]()
Puedes encontrar el código completo de esta rotación en 2D en nuestro GitHub:
Pensando en tres dimensiones
En este punto hemos aprendido a rotar un punto en dos dimensiones. Para cumplir nuestro objetivo final de rotar un punto en tres dimensiones simplemente hay que extender nuestra rotación 2d a cada plano tridimensional:
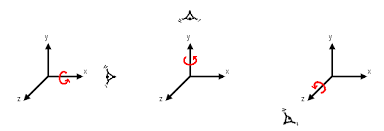
El problema se resolvería haciendo tres rotationes en 2D, cambiando el plano de observación en cada caso, vamos a llamarlas rotacionX, rotacionY y rotacionZ.
Por tanto rotar un punto en tres dimensiones supone la rotación en los ejes XYZ de cada componente de ese vértice. Os invito a hacer el desarrollo completo por vuestra parte.
Para abreviar y siguiendo nuestro ejemplo de código estas serían las tres funciones que nos darían la rotación de un vértice en el espacio:
vertice rotarEjeX(vertice V, double degrees) {
double rads = degreesToRadians(degrees);
vertice A;
A.x = 1 * V.x;
A.y = cos(rads) * V.y + sin(rads) * V.z;
A.z = -sin(rads) * V.y + cos(rads) * V.z;
return A;
}
vertice rotarEjeY(vertice V, double degrees) {
double rads = degreesToRadians(degrees);
vertice A;
A.x = ( cos(rads) * V.x ) - ( sin(rads) * V.z );
A.y = 1 * V.y;
A.z = ( sin(rads) * V.x ) + ( cos(rads) * V.z );
return A;
}
vertice rotarEjeZ(vertice V, double degrees) {
double rads = degreesToRadians(degrees);
vertice A;
A.x = ( cos(rads) * V.x ) + ( sin(rads) * V.y );
A.y = ( -sin(rads) * V.x ) + ( cos(rads) * V.y );
A.z = 1 * V.z ;
return A;
}Con ellas tenemos todo lo necesario para rotar todos los vértices de nuestro modelo 3D. Retomando nuestro ejemplo de código en el que cargabamos todos los vértices de Suzanne, añadiremos la rotación de sus vértices:
for (int i = 0; i<=1448; i++) {
vertice t;
t = mueveVertice(v[i], 0, 0, 3);
t = rotarEjeX(t, 0);
t = rotarEjeY(t, 0);
t = rotarEjeZ(t, 90);
point2d p = perspectiveDivision(t);
SDL_RenderDrawPoint(renderer, p.x, p.y);
}
SDL_RenderPresent(renderer);
Se puede observar como se realiza una rotación de 90º en el ejeZ. Como vemos a continuación el resultado es la rotación en ese eje de la cabeza de Suzanne:
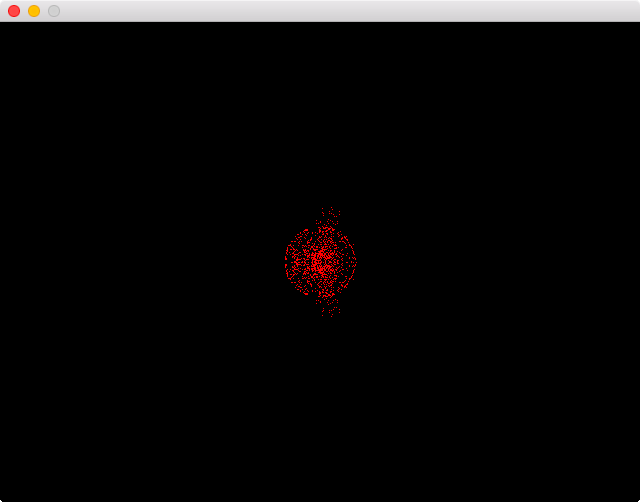
Podéis encontrar el código completo utilizado en este artículo en GitHub:
Resumen
En este post hemos visto como mover y rotar un vértice en el espacio. Con este conocimiento podremos mover y rotar nuestros modelos 3D en el espacio moviendo y rotando cada uno de sus vértices individualmente.
En el siguiente artículo aprenderemos a construir una malla a nuestro modelo 3d, uniendo con líneas los vértices en el espacio.

