Rasterización del triángulo
Bienvenidos de nuevo. En el artículo anterior en lugar de avanzar en nuestro engine, preferí hacer una pausa para destacar la importancia del uso de matrices, ya que es el estándar que encontraremos por todos lados para rotar vértices.
Hoy vamos a continuar hacia nuestro objetivo, detallando el trabajo necesario para rellenar nuestros triángulos, ya sea de un color, un degradado o una textura.
Hasta ahora, hemos visto como dibujar la malla de los triángulos que conforman un modelo. El resultado es creible y realista, pero necesitamos rellenar cada triángulo para conseguir un resultado mas sólido. El término bajo el que se agrupan los conceptos que vamos a utilizar, se llama: rasterización, que en definitiva consiste en el tratamiento de cada pixel en el interior de un triángulo.
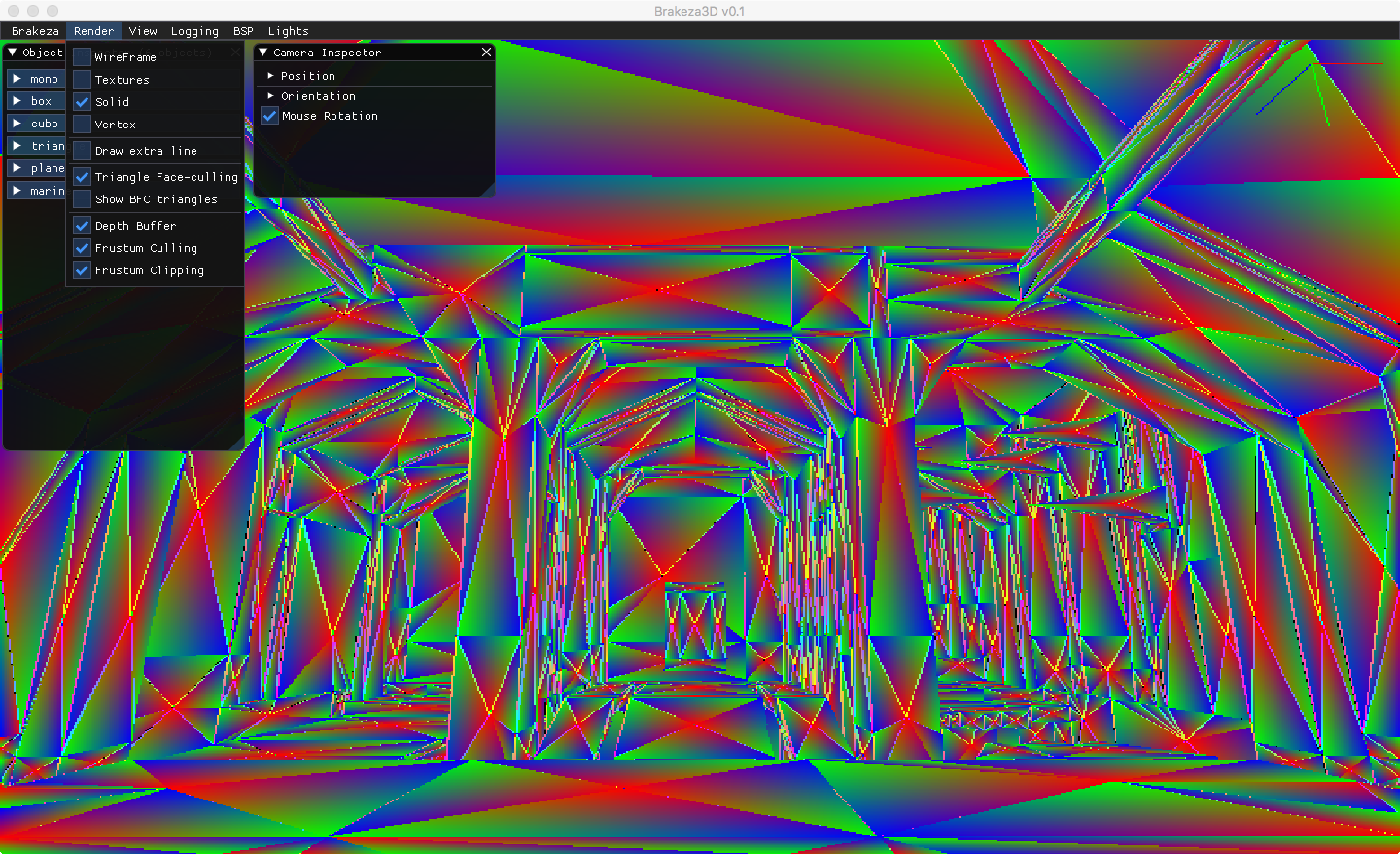
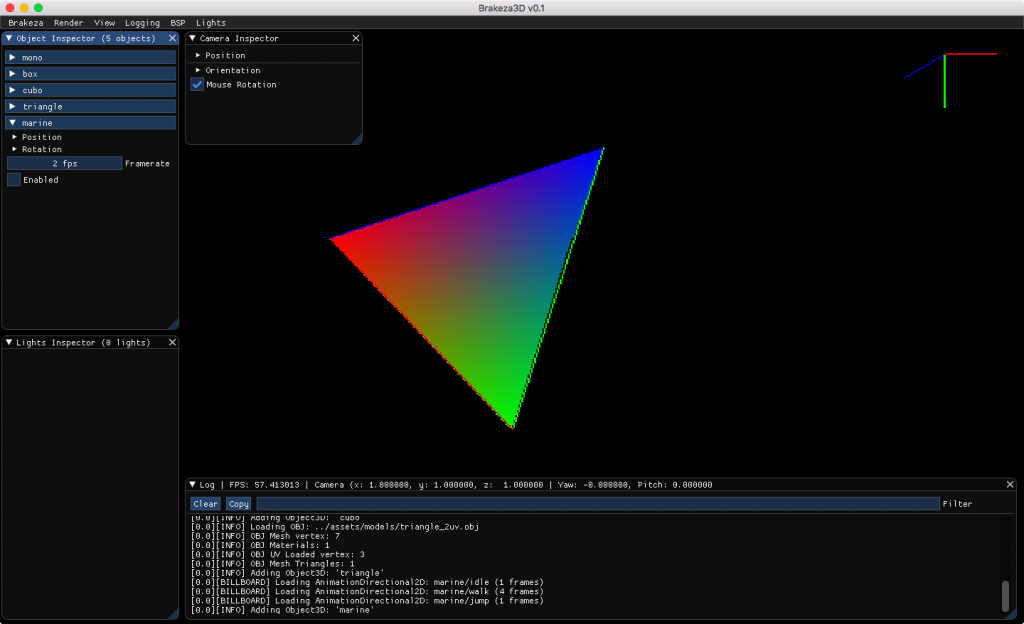
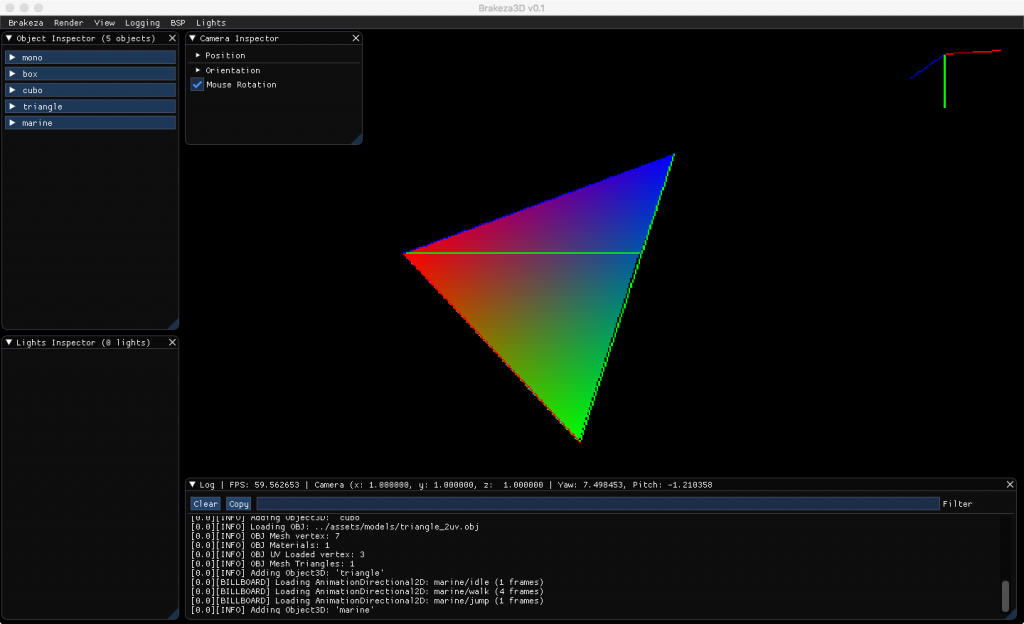
Nuestro primer objetivo, será rellenar un triángulo de un único color, pero habremos terminado nuestro rasterizador cuando seamos capaces de dibujarlo con un degradado interno, donde cada vértice apunte hacia una componente del color RGB:
División del triángulo
Cuando dibujamos el wireframe de un triángulo, apenas nos teníamos que preocupar de agrupar sus vértices de la forma -12-, -23- y -31-, y dibujar líneas una vez conocíamos sus coordenadas en pantalla. Ahora, en su lugar, debemos de ser capaces de recorrer cada píxel en el interior del triángulo.
Supongamos que llamamos A, B y C a los 3 vértices de un triángulo. Queremos recorrer cada pixel que se encuentre en el interior de los vectores AB, CB y CA. Obviamente descartaremos soluciones de fuerza bruta que vayan testeando si un pixel (x, y) se encuentra en el interior del mismo.
La aproximación estándar para conseguir este objetivo requiere empezar de dos posibles situaciones:
- El triángulo que estámos dibujando tiene la base plana (BottomFlat)
- El triángulo que estamos dibujando tiene su alto plano (TopFlat)
Como ya muchos estaréis pensando, casi nunca se cumplirá que el triángulo que estémos dibujando sea perfectamente plano, ya sea en la base o en su alto… asi que ¿Qué me estás contando Edu?.
Pues efectivamente, habremos de detectar si el triángulo que vamos a dibujar se encuentra en alguno de los dos casos descritos arriba, en ese caso, continuaremos con su rasterización, en caso contrario dividiremos el triángulos en dos, donde uno tendrá la base plana y el otro el alto plano y podremos continuar con la rasterización.
Como podéis ver en la imagen superior, la rasterización de nuestro triángulo, requiere partirlo en dos, para que cumplan los requisitos indicados (BottomFlat o TopFlat).
A continuación, os muestro el código de Brakeza3D que realiza este trabajo:
// y obtenemos los puntos en la proyección 2d
Point2D v1 = this->As;
Point2D v2 = this->Bs;
Point2D v3 = this->Cs;
// Ordenamos los vertices y puntos por su valor en 'y'
Maths::sortPointsByY(v1, v2, v3);
if (v2.y == v3.y) {
this->scanBottomFlatTriangle(v1, v2, v3);
} else if (v1.y == v2.y) {
this->scanTopFlatTriangle(v1, v2, v3);
} else {
// En este caso vamos a dividir el triángulo en dos
// para tener uno que cumpla 'bottomFlat' y el otro 'TopFlat' y necesitamos un punto extra para separar ambos
int x = (int) (v1.x + ((v2.y - v1.y) / (v3.y - v1.y)) * (v3.x - v1.x));
int y = (int) v2.y;
Point2D v4(x, y);
this->scanBottomFlatTriangle(v1, v2, v4);
this->scanTopFlatTriangle(v4, v2, v3);
}Podemos observar como inicialmente se ordenan los vértices del tríangulo por su componente Y (los vértices mas arriba primero). A continuación, se determina si el triángulo es BottomFlat o TopFlat, con unas simples comprobaciones de la componente Y. Si el triángulo no es ni uno ni otro, calculamos el nuevo punto y creamos dos nuevos triángulos, ahora ya si, BottomFlat y TopFlat, que pueden continuar su rasterización.
Os presento a continuación el método scanTopFlatTriangle:
void Triangle::scanTopFlatTriangle(Point2D pa, Point2D pb, Point2D pc)
{
float invslope1 = (pc.x - pa.x) / (pc.y - pa.y);
float invslope2 = (pc.x - pb.x) / (pc.y - pb.y);
float curx1 = pc.x;
float curx2 = pc.x;
for (int scanlineY = (int) pc.y; scanlineY > pa.y; scanlineY--) {
this->scanLine(curx1, curx2, scanlineY);
curx1 -= invslope1;
curx2 -= invslope2;
}
}Y ahora scanBottomFlatTriangle:
void Triangle::scanBottomFlatTriangle(Point2D pa, Point2D pb, Point2D pc)
{
float invslope1 = (pb.x - pa.x) / (pb.y - pa.y);
float invslope2 = (pc.x - pa.x) / (pc.y - pa.y);
float curx1 = pa.x;
float curx2 = pa.x;
for (int scanlineY = (int) pa.y; scanlineY <= pb.y; scanlineY++) {
this->scanLine(curx1, curx2, scanlineY);
curx1 += invslope1;
curx2 += invslope2;
}
}Ambas funciones, suman (scanBottomFlatTriangle) o restan (scanTopFlatTriangle) por cada avance en el eje Y, el valor de la pendiente (invslope) a un acumulador, lo que nos determina los extremos en el eje X para cada posición Y.
Con esta eficaz técnica, procesaremos los triángulos BottomFlat de arriba abajo, y de izquierda a derecha y los triángulos TopFlat de abajo arriba y de izquierda a derecha.

Recorrido por los píxeles de un triángulo BottomFlat o TopFlat
Los mas observadores, habréis visto la función scanLine(curx1, curx2, scanlineY). Esta será la encargada de recorrer horizontalmente la línea de píxeles que hay en el triángulo para una coordenada Y dada.
Técnicamente ya tenemos todo lo necesario para recorrer todos los píxeles del interior de nuestro triángulo. Podríamos darle un color uniforme al mismo. Es un gran avance, pero en un futuro no muy lejano, desearemos dotar a nuestro triángulo de una bonita textura y en un futuro un poco mas lejano desearemos calcular la luz que incide en cada píxel. Para ello profundizaremos un poco mas en los cálculos sobre cada píxel en el interior de nuestro amado triángulo 🙂
Coordenadas baricéntricas del triángulo
Podría pasaros el link de la wikipedia sobre las coordenadas baricentricas, pero lo cierto es que es un insufrible galimatías que tardaréis un rato en entender, salvo que estéis acostumbrados a trabajar con notación matemática.
Este link del Código Gráfico me ayudo a entenderlo mucho mejor.
En el fondo lo que vamos a hacer es calcular tres valores, que llamaremos: alpha, gamma y theta, los cuales serán de un rango [0-1] y que como dato, su suma siempre será uno.
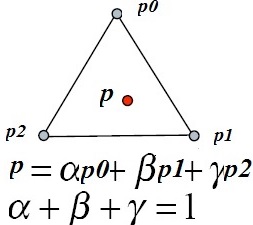
Coordenadas baricéntricas
Desde el punto de vista matemático, calcularemos el rango [0-1] entre dos vértices del triángulo, en función del punto p. Es decir, calcularemos el rango [0-1] entre p0-p1 (alpha), entre p1-p2 (gamma) y p3-p0 (theta), todos ellos en función del vértice p.
Poder calcular las coordenadas baricentricas de un punto P(x, y) en un triángulo con vértices p1, p2 y p3, nos permite tener un control mucho mayor de la posición que ocupa nuestro píxel dentro del triángulo.
Veámos por ejemplo, como calcular el gradiente RGB de un pixel:
float alpha, theta, gamma;
Maths::getBarycentricCoordinates(alpha, theta, gamma, pointFinal.x, pointFinal.y, As, Bs, Cs);
Uint32 pixelColor = (Uint32) Tools::createRGB(alpha * 255, theta * 255, gamma * 255);En el código superior, se establece la cantidad de rojo, verde y azul que lleva el pixel en función de las coordenadas baricentricas que determinan la posición del mismo en el triángulo. El resultado sería el mostrado en las capturas al inicio del artículo.
El código completo para calcular las coordenadas baricentricas de un triángulo es el siguiente:
void Maths::getBarycentricCoordinates(float &alpha, float &theta, float &gamma, int x, int y, Point2D v1, Point2D v2, Point2D v3)
{
alpha = Maths::barycentricSide( x, y, v2, v3 ) / Maths::barycentricSide( v1.x, v1.y, v2, v3 );
theta = Maths::barycentricSide( x, y, v3, v1 ) / Maths::barycentricSide( v2.x, v2.y, v3, v1 );
gamma = Maths::barycentricSide( x, y, v1, v2 ) / Maths::barycentricSide( v3.x, v3.y, v1, v2 );
}float Maths::barycentricSide(int x, int y, Point2D pa, Point2D pb)
{
return (pa.y - pb.y) * x + (pb.x - pa.x) * y + pa.x * pb.y - pb.x * pa.y;
}Os invito a desde cero y sobre el papel, calcular las coordenadas baricéntricas de un punto en un triángulo si tenéis dudas o el código no os resulta aclarador.
El otro gran aporte de las coordenadas baricéntricas, es la posibilidad de calcular la coordenada UV para el mapeo de texturas. De hecho, podríamos utilizarlas contra cualquier mapeo al que estén sometidos los vértices del triángulo.
Volviendo al mapeo UV, el resultado del cálculo sería algo similar a esto:
// UV texture coordinates
float u = alpha * A.u + theta * B.u + gamma * C.u;
float v = alpha * A.v + theta * B.v + gamma * C.v;En el siguiente artículo profundizaremos en la texturización de nuestro triángulo.
Resumen
Hoy hemos abordado una parte crítica en todo motor 3D, la rasterización de sus triángulos.
Hemos esbozado un workflow para procesar el interior de un triángulo píxel a píxel y realizado cálculos en cada píxel para determinar exactamente en que posición estamos (coordenadas baricéntricas) respecto a los tres vértices.
Cabe destacar que la rasterización ocupará gran parte de los ciclos de CPU, ya que aumentamos drásticamente el procesamiento requerido. A partir de ahora toca apretarse el cinturón 😉

