Hoy vamos a hablar de texturas. Con todo lo visto en artículos anteriores, estaríamos preparados para llegar, desde el concepto de píxel, hasta el de modelo 3D proyectado en pantalla, de color sólido o con degradados, pudiendo mover y/o rotar este modelo en el espacio. Grandes avances para tan poca teoría!.
En el último artículo, os hablé sobre la rasterización del triángulo. Una bonita palabra, que agrupaba toda la batalla que hemos de plantear, para pintar el interior de nuestros triángulos, píxel a píxel. Bien sea de color sólido, degradado o textura.
Como ya hemos visto, para pintar nuestro triángulo de color sólido, el rasterizador simplemente pinta el pixel del color deseado, sin necesidad de realizar cálculos adicionales.
Sin embargo, para rellenar nuestro triángulo con un degradado, hablamos de otra herramienta muy útil: las coordenadas baricéntricas, las cuales nos aportan un gradiente de rango [0,1] para cada lado del mismo, en función de un punto P en el interior del triángulo.
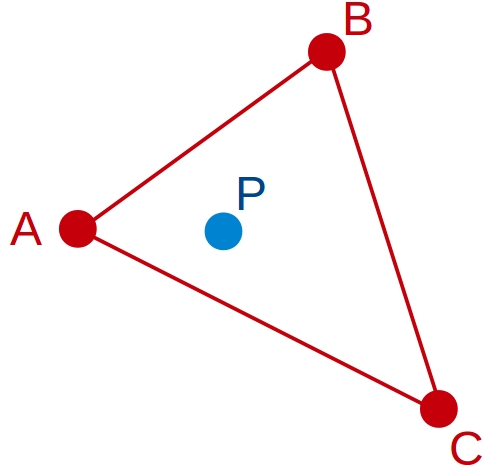
Tomando como referencia la imagen superior: si trazamos una línea perpendicular a cada lado del triángulo hacia P, obtendríamos la coordenada baricéntrica para cada lado.
Por ejemplo, la coordenada baricéntrica del punto P, en el vector AB, sería aprox. 0.3 (a ojo de buen cubero, algo a la izquierda de la mitad, que sería 0.5).
Si repetimos la operación para cada lado o vector del triángulo, obtendríamos nuestras tres coordenadas baricéntricas, las que denonimaremos: alpha (AB), gamma (BC) y thetha (CA). En definitiva las coordenadas baricéntricas, nos aportan 3 pesos, los cuales nos permiten identificar cualquier posición de un píxel en nuestro triángulo.
Tenéis el código que calcula las coordenadas baricéntricas de un triángulo en el capítulo anterior. Os recomiendo atar bien este concepto antes de continuar.
Mapeado UV
Seguro que todos habréis escuchado o leído alguna vez este término. El mapeado UV, y valga la redundancia, no es mas que el mapeado de los vértices de un triángulo contra unas coordenadas que en este caso, corresponden a un plano 2D.
Cuando mapeamos información a vértices, se suele denominar a esta: atributos. De hecho existen múltiples tipos de atributos mapeables a un vértice, no solo los referentes a su textura, por ejemplo, mapas de luz. Por tanto, podemos decir que UV, no son más que atributos mapeados contra los vértices del triángulo.
¿Y qué tipo de atributo representa UV?
Aunque existen mapeados 1D y 3D, el caso habitual, será mapear nuestros triángulos contra una textura de imagen, es decir, un plano 2D al fin y al cabo. ¿Cuantas coordenadas necesito para posicionar un punto en 2D? Pues dos. Alguien decidió en su momento, que una de estas coordenadas se llamaría U y la otra V.
Lo primero que debemos tener en cuenta, es que las coordenadas UV se almacenan mediante un rango [0, 1], una asociada a la horizontal y la otra asociada a la vertical de la textura.
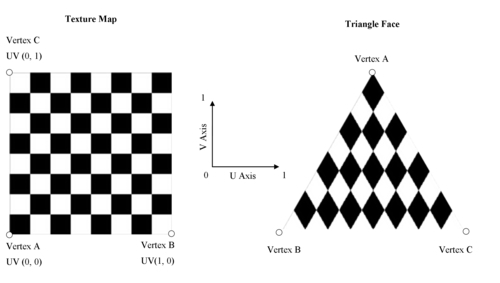
Otro detalle a tener en cuenta, es la orientación de los ejes U y V. En la imagen superior podéis observar como la coordenada V(0) parte de la esquina inferior izquierda de la textura y crece hacia arriba y la coordenada U(0) crece hacia la derecha. Esto no siempre es así. Es simplemente una convención que hemos de mantener a la hora de implementar nuestra texturización o respetar la convención de otros, si estáis texturizando información generada por otros programas tipo Blender.
Ya que he mencionado Blender y que hace bien poco ha salido su versión 2.80, veámos como almacena este software la información UV de cada uno de sus vértices:
# Blender v2.78 (sub 0) OBJ File: 'triangle.blend' # www.blender.org mtllib triangle_2uv.mtl o Plane v -1.000000 0.000001 1.00000 v 1.000000 0.000001 1.000000 v 0.035049 0.001838 -0.988047 vt 1.0000 1.0000 vt 0.0000 0.0000 vt 1.0000 0.0000 vn 0.0000 1.0000 0.0009 usemtl None s off f 1/1/1 2/2/1 3/3/1
Podéis observar como se distinguen dos bloques de información: el primer bloque de información comienza por la letra v y el segundo con las letras vt. Es este segundo grupo de información, el que aporta las coordenadas UV para el vértice que ocupa la misma posición en el grupo con la letra v. Tal que así:
v -1.000000 0.000001 1.00000 -> UV: vt 1.0000 1.0000 v 1.000000 0.000001 1.000000 -> UV: vt 0.0000 0.0000 v 0.035049 0.001838 -0.988047 -> UV: vt 1.0000 0.0000
¿Cómo averiguo las UV para un píxel del triángulo?
Es ahora cuando haremos uso de las coordenadas baricéntricas. En el anterior artículo aprendimos a calcular alpha, gamma y thetha para cada píxel en el interior del triángulo.
Tenéis que daros cuenta, que las coordenadas baricéntricas del triángulo que estámos rasterizando, nos sirven para obtener tres pesos. Con estos pesos que podemos determinar exactamente, en que posición nos encontramos entre tres vértices. Dicho de otra forma, podemos usar las coordenadas baricéntricas contra los tres vértices de la textura (contra sus atributos) para obtener la coordenada UV del píxel que estamos procesando.
¿Recordáis como obteníamos el RGB del pixel que estamos procesando?:
float alpha, theta, gamma; Maths::getBarycentricCoordinates(alpha, theta, gamma, pointFinal.x, pointFinal.y, As, Bs, Cs); Uint32 pixelColor = (Uint32) Tools::createRGB(alpha * 255, theta * 255, gamma * 255);
Pues de forma similar, para obtener nuestra coordenada UV haremos algo así:
float u = alpha * As.u + theta * Bs.u + gamma * Cs.u; float v = alpha * As.v + theta * Bs.v + gamma * Cs.v;
Como podéis ver, las coordenadas baricéntricas pueden utilizarse contra cualquier atributo existente en nuestros vértices para hallar el valor que corresponde al pixel actual.
Con las coordenadas UV bajo el brazo, solo necesitamos una función que determine el color en la textura para la coordenada UV dada. Esto es prácticamente trivial, veámos algo de código:
int Tools::getXTextureFromUV(SDL_Surface *surface, float u) { return surface->w * u; } int Tools::getYTextureFromUV(SDL_Surface *surface, float v) { return surface->h * v; }
Uint32 Tools::readSurfacePixelFromUV(SDL_Surface *surface, float u, float v) { return Tools::readSurfacePixel( surface, Tools::getXTextureFromUV(surface, u), Tools::getYTextureFromUV(surface, v) ); }
No me detendré en como abrir imágenes para su almacenamiento como arrays de píxeles. Podéis obtener esa información en los tutoriales de LazyFoo.
¿Hemos terminado?
Por desgracia, no hemos terminado. La culpable es la perspectiva. Si renderizamos un mundo complejo con texturas tal y como hemos descrito, observaremos que hay irregularidades. Veámos de que se trata:
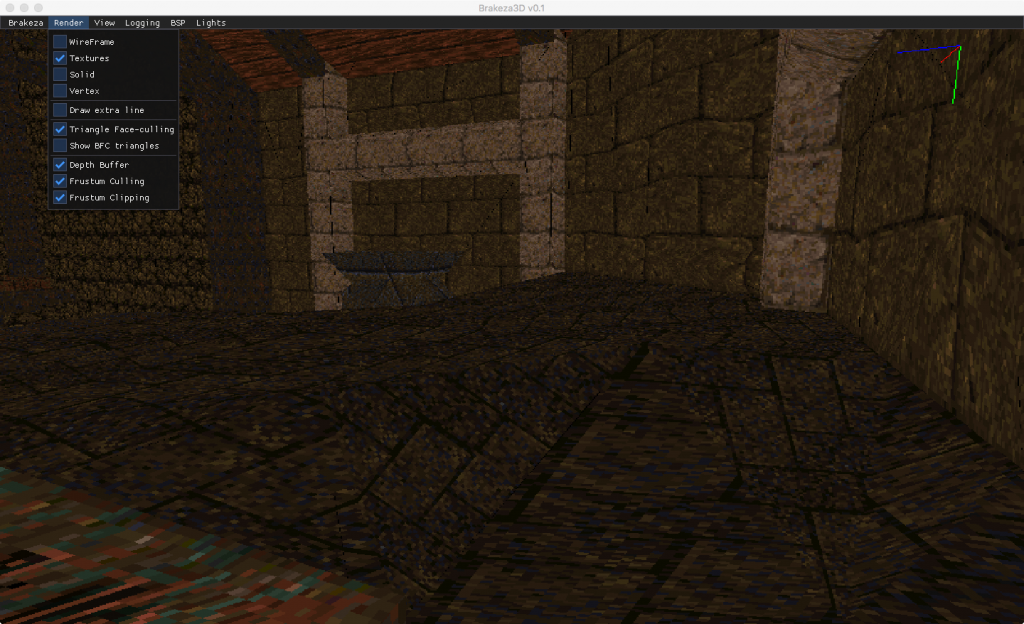
Podeís ver como las líneas sufren deformaciones, no se mantienen paralelas y en movimiento, se produce una especie de efecto caleidoscópio nada deseable 😛
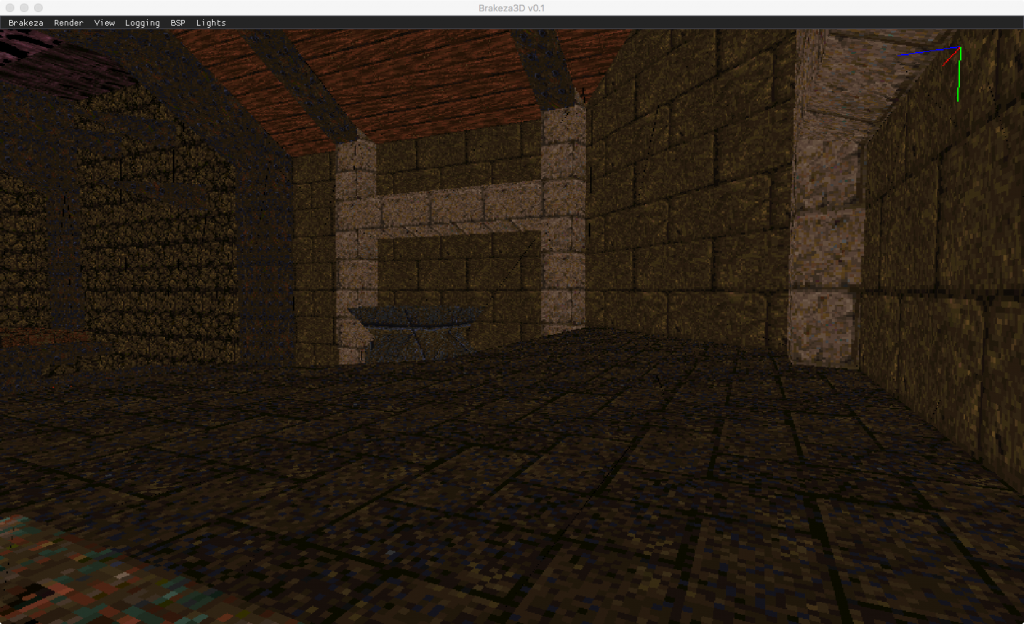
Arriba podéis ver el mismo software, que implementa la corrección de perspectiva y donde ya no se observan irregularidades.
¿Cual es el problema?
¿Recordáis el artículo donde os hablaba de la perspectiva?. Lo resumíamos, como el hecho de que las cosas se ven mas pequeñas cuanto mas lejos están.
El uso de coordenadas baricéntricas sin mas, no tiene en cuenta la perspectiva y situaría, por ejemplo, en 0.5 exacto la mitad entre dos vértices AB, aunque en la proyección de este vector en pantalla, su mitad será muy diferente. Veámos un ejemplo:

Supongamos que la imagen superior es un plano texturizado, en perspectiva podría observarse tal que así:
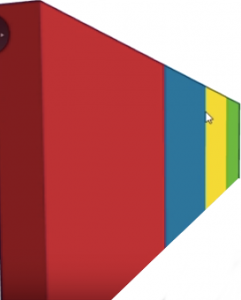
Se puede observar claramente, como la mitad del plano en perspectiva, no se corresponde con la mitad real entre los extremos de las líneas (que sería el valor que nos proporciona la coordenada baricéntrica), por tanto, debemos realizar una corrección, la corrección de perspectiva.
Para ello utilizaremos la profundidad, es decir la posición Z que ocupa el píxel en el mundo. El código que nos permite hacer la corrección de perspectiva a nuestras coordenadas UV es el siguiente:
float z = 1 / ( alpha * (1/Ac.z) + theta * (1/Bc.z) + gamma * (1/Cc.z) ); // Correct perspective mapping float u = ( alpha * (Ac.u/Ac.z) + theta * (Bc.u/Bc.z) + gamma * (Cc.u/Cc.z) ) * z; float v = ( alpha * (Ac.v/Ac.z) + theta * (Bc.v/Bc.z) + gamma * (Cc.v/Cc.z) ) * z ;
Si recordáis del segundo artículo, dividir entre Z es básicamente lo único que hemos de hacer para obtener la perspectiva de un vértice, hacemos el equivalente con las coordenadas UV.
UV fuera de rango
Esto es algo que no se suele mencionar, pero las coordenadas UV no siempre se restringen al rango [0, 1]. En ocasiones, encontraréis valores que se salen de estos rangos.
Generalmente esto indica «repetición» y podréis ignorar la parte entera de la coordenada U o V que procesáis. Es una práctica muy común.
Otra cosa muy habitual es jugar con el signo de la coordenada UV, cuando es menor, invertimos su valor (1-u o 1-v) para obtener una textura «espejo» (mirrored):
En el siguiente ejemplo, las texturas del indicador de dirección hacia la habitación, se invierten mediante este mecanismo:

El código completo de texturizado UV del Quake sería:
// cálculo de profundidad float z = 1 / ( alpha * (1/Ac.z) + theta * (1/Bc.z) + gamma * (1/Cc.z) ); // Corección de perspectiva float u = ( alpha * (Ac.u/Ac.z) + theta * (Bc.u/Bc.z) + gamma * (Cc.u/Cc.z) ) * z; float v = ( alpha * (Ac.v/Ac.z) + theta * (Bc.v/Bc.z) + gamma * (Cc.v/Cc.z) ) * z ; float ignorablePartInt; if (!std::signbit(u)) { u = modf(abs(u) , &ignorablePartInt); } else { u = 1 - modf(abs(u) , &ignorablePartInt); } // Check for inversion U if (!std::signbit(v)) { v = modf(abs(v) , &ignorablePartInt); } else { v = 1 - modf(abs(v) , &ignorablePartInt); }
Resumen
Hemos aprendido las bases del mapeado UV. Aprovechando lo aprendido en el artículo del rasterizador de triángulos, hemos usado las coordenadas baricéntricas junto con la corrección de perspectiva, para obtener unas coordenadas 2D válidas que poder llevar a la pantalla. Ahora ya podemos texturizar nuestros triángulos!






Deja una respuesta