Difusión, emisión y especularidad

Buenas de nuevo! Hoy vamos a continuar profundizando en la implementación de nuestro sistema de iluminación 3D. En el pasado, hablábamos sobre los tipos principales de luces y sus propiedades básicas, tomando como objetivo simple y principal, el colorear adecuadamente los pixels en función del color, la distancia y ángulo a la luz.

En esta ocasión vamos a profundizar en cómo se comporta la luz al golpear un punto de una superficie en el espacio y las posibilidades que esto nos ofrece.

Materiales

Hasta ahora para colorear un pixel en el espacio no disponíamos más que de la intensidad de una luz (un escalar) y el color de dicho pixel en su textura (un RGB) que aplica a dicho triángulo. Mediante aritmética de colores obteníamos otro RGB resultante. Así con cada punto de luz hasta obtener un color final.

De esta manera, si tuviéramos cinco luces apuntando a un punto, tendríamos cinco modificaciones de color antes de obtener el resultado. Perfecto!

Hasta ahora observamos que la única propiedad que manejamos del objeto que estamos iluminando, es su color. En el mundo real, las superficies tienen muchas más propiedades que determinan el comportamiento del reflejo de luz.

Pongamos por ejemplo la pantalla apagada una tablet, ciertamente es negra, pero si observamos desde cierto ángulo, no veremos el 100% del mismo color, esta tendrá reflejos y/o rugosidades que varían resultado final. Ejemplo:

Para agrupar todas estas propiedades, hoy en día es muy habitual encontrarnos el concepto de “material“, que no es más que un conjunto de propiedades que modifican simultáneamente el comportamiento de la luz al golpear un objeto. Encontraremos este concepto en cualquier programa de 3D.

Vamos a presentar tres de las propiedades principales que se suelen encontrar en cualquier material y a profundizar en los detalles de implementación, me estoy refiriendo a: La difusión, la emisión y la especularidad. Vamos con ello!

Difusión

Una superficie difusa es aquella en la que al ser golpeada por un rayo de luz, esta sale reflejada en direcciones aleatorias. Pero…no suena muy bien esto, aleatorias? qué hacemos?

Una solución razonable, es asumir que la luz sale disparada en todas las direcciones uniformemente. Esto se conoce como iluminación Lambertiana. Jaque mate! Bien por Lambert!

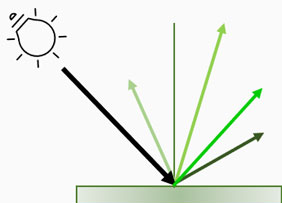
Las iluminaciones de este tipo tienen una cualidad muy concreta y fácil de observar: El resultado del punto de superficie iluminado, no varía respecto al observante. En la siguiente figura observamos como la misma esquina superior derecha del cubo, se mantiene intacta en lo relativo al color de sus pixeles en función del ángulo donde observemos el cubo.

En resumen, podemos entender el canal difuso de un material, como la mezcla de su color normal de textura y el aportado por la luces que lo iluminan, es decir, el mapeado UV de toda la vida contra una textura de color, más el aporte de sus luces.

Emisión

Pensemos que algunos objetos pueden emitir luz, además de reflejarla!.

Un objeto puede ser parcialmente difuso y parcialmente emisivo!. La predominancia de color para píxeles emisivos, siempre vendrá determinada por la intensidad del color de emisión.

El canal de emisión suele presentarse como una textura separada, con sus específicas coordenadas UV, mapeando las zonas que emiten luz del objeto. Los colores procedentes de esta textura los modularemos con una componente (un multiplicador) para variar la intensidad de la emisión.

Por ejemplo, en la imagen superior se observa una nave espacial, cuyos “propulsores” mapean contra una textura específica para el canal de emisión, pudiendo alterar su componente de intensidad, para transladar aceleración/desaceleracíón. A su izquierda la textura de difusión que aplica el color normal.

Las superficies con emisión tampoco varian su resultado en función de la posición del observador.

Especularidad

Una superficie especular es aquella en la que la luz es reflejada en una dirección determinada. A diferencia de las superficies con difusión y emisión, en una superficie especular, el resultado varia en función de la posición del observador. 

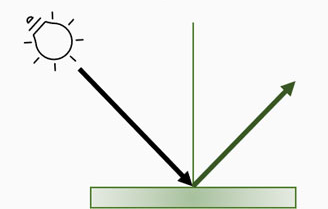
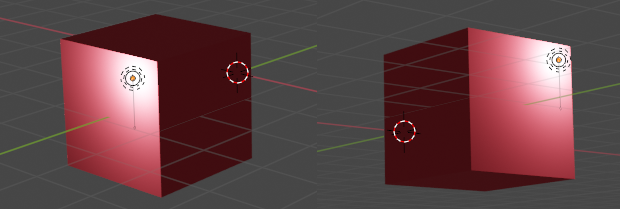
En la imagen siguiente, observamos reflejos especulares y podemos observar como desde el punto de vista que tomamos la captura, el reflejo cae hacia la esquina superior derecha tomando como referencia la luz:

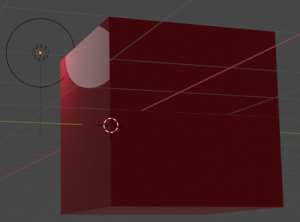
Sin embargo, si cambiamos nuestro ángulo de cámara, el reflejo especular cae hacia la esquina inferior izquierda:

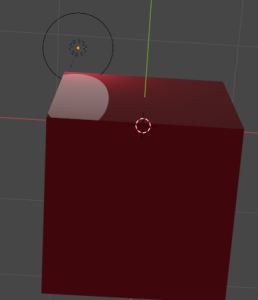
Jugando con la especularidad podemos conseguir algunos efectos bastante interesantes.

Generalmente se la entiende como una operación global a nivel de superficie, es decir, se asume que todos los pixels de dicha superficie reflejan la luz en la misma dirección. Por comodidad, el ángulo de reflexión que se utiliza normalmente corresponde al ángulo mitad entre el que forman el observador y la luz, respecto del punto de incidencia.

Sin embargo, existen técnicas que se apoyan en la especularidad per-pixel para conseguir efectos mucho más vistosos. El ejemplo más conocido sería el bump mapping o normal mapping, donde aportaremos una dirección de reflejo específica por pixel, también a través de una ‘textura’ especial:

En el caso del normal mapping, la dirección de reflejo de cada pixel vendrá determinada por el vector aportado a través de una textura (unitario). Las componentes x, y, z del vector se mapean contra las componentes RGB del color. Buen truco!

Implementación

Para poder sintetizar bien esta parte, recomiendo repasar los posts anteriores, principalmente lo relativo a rasterizador, texturizado UV y luces, además de entender con soltura las operaciones básicas con vectores (aritmética, dot, cross…) y matrices.

Iluminación de superficies difusas

Realmente ya lo hemos visto todo aquí en los links mencionados, no obstante haremos un repaso. Las variables que manejábamos son:

• Coordenada 3D de la superficie en el espacio que estamos renderizando. La llamaremos Q
• Color de textura RGB. Lo llamaremos c
• Color de luz RGB. Lo llamaremos c0
• Coordenada 3D en la que se sitúa la luz. La llamaremos P
• Vector dirección de emisión de la luz desde su posición. Lo llamaremos R
• Constantes linear/cuadrática de la luz. Las llamaremos kc, kl y kq
• La distancia entre P y Q. La llamaremos d 
• Vector unitario que va desde Q hasta P. Lo llamaremos L 
• El spotLight component. Que llamaremos p

La incógnita es la intensidad a aplicar dicha luz. La cual llamaremos C

La expresión que debemos implementar es:

C = max{-R * L, 0}^p / (kc + kd *d + kq * d^2)

donde L sería:

L = (P - Q) / (|P-Q|)

Una vez obtenemos C podemos utilizarla para mezclar el color c con el color c0

Finalmente el color RGB del pixel para esta luz sería: 

finalRGB = C * c + c0

Iluminación de superficies con emisión

Iluminar este tipo de superficies equivale a un mapeo UV estándar, simplemente consultando otra textura. No profundizaremos en ello.

Simplemente destacaremos que la emisión dispone de una constante ke que representa la intensidad con la que emite dicha luz.

Las variable que manejaremos serán:

• Color de textura RGB. Lo llamaremos c
• Constante de emisión de la textura. La llamaremos ke

finalRGB = Ke * c0

Iluminación de superficies con reflejos especulares

Este tipo de reflejos requiere ir un pasito más allá, tampoco demasiado!. Las variables que manejaremos son:

• Coordenada 3D de la superficie en el espacio que estamos renderizando. La llamaremos Q
• Coordenada 3D en la que se sitúa la luz. La llamaremos P
• Vector en la dirección de emisión de la luz desde su posición. Lo llamaremos R
• El vector normal de la superficie. Lo llamaremos N
• Vector hacia el observador (desde Q). Lo llamaremos V
• Vector de reflejo de la superficie (desde Q). Lo llamaremos R
• Vector hacía la luz (desde Q). Lo llamaremos L
• Exponente de contribución especular. Lo llamaremos m
• Tinte especular RGB. Lo llamaremos cs

La incógnita será resolver intensidad de cs para el pixel que estamos renderizando. La llamaremos C

La expresión es la siguiente:

C = max{R*V, 0}^m * (N*L>0)

La expresión (N*L>0), es una expresión booleana que evalua a 1 si es verdad y a 0 en caso contrario. Evita reflejos procedentes de luces totalmente verticales.

Ya con C calculado podemos obener la cantidad de color aportado por dicha especularidad:

finalRGB = C * cs

Ejemplo completo

Veamos el código que he implementado para ello. Os adelanto que es una transcripción literal de lo explicado arriba.

Por un lado, añadiremos al rasterizador, la capacidad de iterar un pixel sobre todas las luces para ir modificando el color original de la textura.

Color ComponentRender::processPixelLights(Triangle *t, Fragment *f, Color c)
{

    if (!this->lightpoints.empty()) {
        // Coordenadas del punto que estamos procesando en el mundo (object space)
        float x3d = f->alpha * t->Ao.x + f->theta * t->Bo.x + f->gamma * t->Co.x;
        float y3d = f->alpha * t->Ao.y + f->theta * t->Bo.y + f->gamma * t->Co.y;
        float z3d = f->alpha * t->Ao.z + f->theta * t->Bo.z + f->gamma * t->Co.z;

        Vertex3D D = Vertex3D(x3d, y3d, z3d); // Object space

        for (auto & lightpoint : this->lightpoints) {
            if (!lightpoint->isEnabled()) {
                continue;
            }

            c = lightpoint->mixColorDiffuse(c, D, f);
            c = lightpoint->mixColorSpecular(c, D, f);
        }

    return c;
}

Sobre cada pixel/luz llamaremos a las funciones que harán el “blend” del color, uno para el reflejo difuso y otro para el especular. Este sería su código:

Color LightPoint3D::mixColorDiffuse(Color colorTexture, Vertex3D Q, Fragment *fragment)
{
    const float distance = Maths::distanceBetweenVertices(this->getPosition(), Q);

    Vertex3D P = this->getPosition();
    Vertex3D R = this->AxisForward();

    Vector3D Light = Vector3D(Q, P);
    Vertex3D L = Light.normal();

    float C = powf(fmaxf(R * L, 0), this->p) / (this->kc + this->kl * distance + this->kq * (distance * distance));

    Color diffuseColor;
    if (C >= 1) {
        diffuseColor = this->color;
    } else {
        diffuseColor = Color::mixColor(colorTexture, this->color, C);;
    }

    return diffuseColor;
}

Y el código para la mezcla especular:

Color LightPoint3D::mixColor(Color c, Vertex3D Q, Fragment *f)
{
    Vertex3D P = this->getPosition();

    Vector3D Light = Vector3D(Q, P);
    Vector3D Viewer = Vector3D(Q, getComponentCamera()->getCamera()->getPosition());

    Vertex3D Ls = Light.getComponent().getInverse();
    Vertex3D V = Viewer.getComponent();
    Vertex3D N = Vertex3D(f->normalX, f->normalY, f->normalZ);
    Vertex3D H = this->getHalfWay(Vector3D(Q, P).getComponent() + V);

    float booleanCondition = 1;
    if (N * Ls > 0) {
        booleanCondition = 0;
    }

    const float K = powf(fmaxf(N * H, 0), this->specularComponent) * booleanCondition;

    Color specularColor = Color::mixColor(c, this->specularColor, K);

    return Color::mixColor(specularColor, c, 0.5);
}

Aritmética RGB

Estoy escribiendo con mucha ligereza sobre las operaciones RGB, aparentando que es un tema trivial y sin importancia, cuando realmente tiene su enjundia. La realidad si es que las componentes RGB de un color son números, como ya hemos hablado otras veces y efectivamente podemos sumarlos, restarlos y multiplicarlos. Lo que no significa que el resultado corresponda con el que la física real nos ofrece.

Existen dos estrategias principales para operar con colores: 

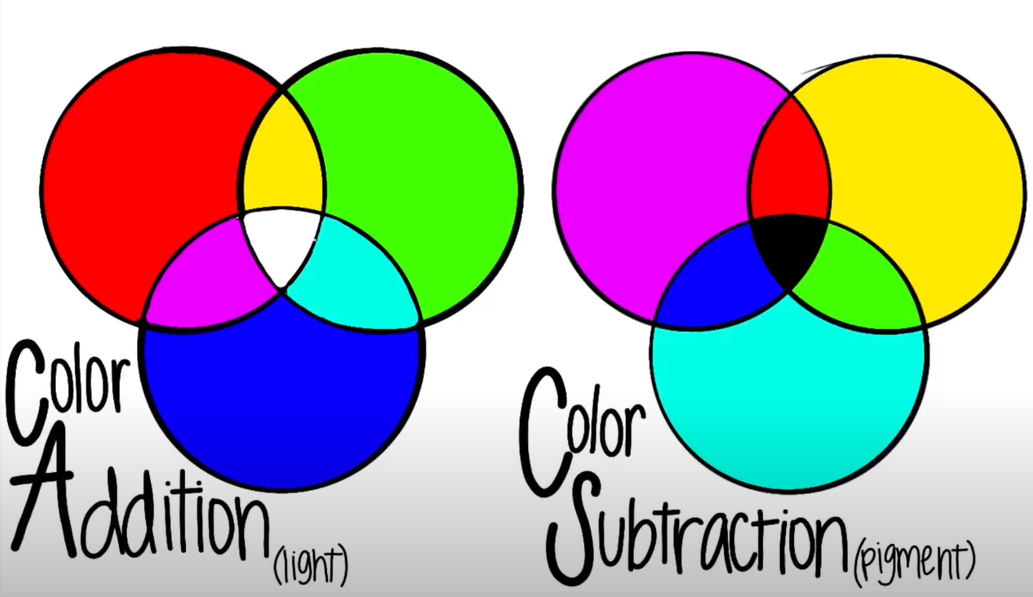
Como podéis observar la suma de colores tiende a blanco (máximo FF, 255), y la substraction tiende a zero, osea negro. La elección de una u otra estrategia modificará los colores resultantes, pudiendo estos sobresaturar de no ser corregidos con algún factor de escala. Este es el motivo exacto de esta parte del código, evitar la saturación máxima (asumiendo el 100% del reflejo del color de la luz como tal escenario)

Color diffuseColor;
if (C >= 1) {
    diffuseColor = this->color;
} else {
    diffuseColor = Color::mixColor(colorTexture, this->color, C);;
}

Dicho esto, os presento mi función de mezcla de colores:

Es en resumen una estrategia aditiva, que mezcla el segundo color con el primero en base a una intensidad dada

Color Color::mixColor(Color &c1, Color &c2, float c2Intensity)
{
    float originIntensity = 1 - c2Intensity;
    return Color(
        (c2.r * c2Intensity) + (c1.r * originIntensity),
        (c2.g * c2Intensity) + (c1.g * originIntensity),
        (c2.b * c2Intensity) + (c1.b * originIntensity)
    );
}

Resultado

Podemos ver el resultado de un spotLight contra un plano con el reflejo especular de fondo en el que voy interactuando con las distintas variables que hemos visto arriba:

Resumen

Hemos profundizado en algunas de las propiedades más básicas de la reflexión de la luz y que encontramos constantemente en programas de 3D o incluso 2D. Amén del aporte académico, esta implementación no será demasiado útil en un entorno real, donde este tipo de efectos se delegan absolutamente en APIs que se apoyan en hardware. En nuestro motor 3D vía software, este tipo de efectos reducirá drásticamente la velocidad de frames por segundo.

No puedo dejar de recomendar este libro de Eryc Lengyel, fuente constante de consulta durante este desarrollo: