Buenas de nuevo! En el último post nos alejamos de la programación para experimentar con un sistema de motion capture low-cost. Hoy volvemos al camino discutiendo sobre tres de las estructuras de datos más habituales cuando manejamos geometría 3D y a las que casi cualquier engine moderno da soporte: Las particiones binarias del espacio (BSP), los árboles de octantes (Octrees) y las rejillas (Grid).
¿Qué aportan estas estructuras?
Cualquiera de estas estructuras hacen esencialmente lo mismo: Indexar el espacio, es decir, ordenan los datos de nuestra geometría.
Son estructuras de datos que pueden trabajar conjuntamente con estrategias del tipo «divide y vencerás» donde gracias a su troceado e indexación previa del espacio, podremos tomar decisiones anticipadas sobre dicha geometría. Estas estructuras son aplicables al renderizado, inteligencia artificial, colisiones o sencillamente como elemento optimizador en algún proceso concreto.
Como desarrollador de videojuegos, tendremos que sopesar los pros y los contras de cada una de ellas para elegir la que mejor nos convenga en cada caso.
¿Cual elegir en cada caso?
Una vez más en la vida no encontraremos una solución única y perfecta para todos los escenarios. Estamos ante el tipico tradeoff. Podemos aproximarnos a las bondades de cada una de ellas desde el siguiente enfoque:
- Velocidad de lectura
- Velocidad de creación
La creación de un árbol BSP es compleja de implementar y lenta en su ejecución de creación, aunque una vez creado, su velocidad de lectura sea muy rápida. En sus tripas queda reflejada toda la geometría, por lo que es una estructura INMENSA por defecto y su uso suele estar muy vinculado al renderizado de geometría.
Por otra parte los Octree y Grids son sencillos de implementar y razonablemente rápidos de leer. Estas estructuras no suelen pretenden almacenar toda la geometría, sino más bien almacenar meta-información espacial (por ejemplo vacío o no vacío!), con la que poder implementar otras funcionalidades de mayor nivel. Son estructuras LIGERAS.
Aplicación en renderizado de escenas
Ya hemos hablado en el pasado del Frustum View, esa famosa «pirámide truncada» que delimita la visión de nuestra cámara.
Una gran parte del tiempo un render por software se encarga de descartar la geometría que está fuera del Frustum View, cualquier ayuda que podamos aportar a aliviar esta fase será de vital importancia.
Hagamos un poco de memoria sobre éste proceso: Sabemos que sólo renderizamos triángulos que se encuentren totalmente dentro del Frustum, los que se encontrasen parcialmente fuera/dentro ya habrían sido recortados en la fase de clipping o recortado. Además sabemos que podemos ignorar los que se encuentren «dándonos el culo (back-face culling)». Todo esto es perfecto, pero por ahora nada nos evita tener que procesar TODOS los triángulos de un objeto, para al menos, determinar estos dos puntos que hemos mencionado.
A continuación un ejemplo simplificado de la idea de descartar geometría utilizando Octrees:
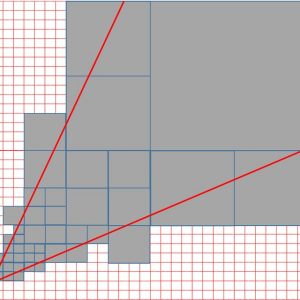
Es aquí donde tiene sentido disponer de la geometría indexada, lo que nos permitirá anticiparnos a estas situaciones y descartar grandes porciones de la geometría antes de enviarlas al rasterizador.
Aplicaciones fuera del renderizado
Estas estructuras de datos serán útiles en cualquier clasificación de datos espaciales que necesitéis.
Cómo programadores 3D habrá situaciones en las que debáis someter una geometría a algún tipo de análisis espacial y aunque siempre nos quedará la fuerza bruta, es decir, analizar cada triángulo/vértice individualmente, no suele ser aplicable en tiempo real, por lo que es interesante el uso de estas estructuras cacheadas para obtener el mismo resultado de forma optimizada.
Voy a intentar explicarlo con un caso de uso: En el pasado ya he hablado algo de la IA en 3D enfocado a un sistema de «Mallas de Navegación». Una malla de navegación nos aporta un «camino» viable sobre una geometría (oséa, el suelo pisable!), correcto.
Pero ¿qué pasa si el personaje puede volar?…eeeh… podemos intuir que necesitamos más información. Necesitamos un análisis volumétrico (esto suena muy top) que nos indique que volúmenes están vacíos y cuales no para poder indicarle a un hipotético algoritmo de pathfinding por donde puede volar dicho personaje.
En definitiva, cualquier dato espacial es susceptible de ser organizado en alguna de estas estructuras de datos con el fin de optimizar su procesamiento en alguna tarea específica. Veamos los detalles de cada una de ellas.
Grids
El grid es la estructura más fácil de visualizar: Sobre un modelo dado, hayaremos su BoundingBox y este lo dividiremos en tantos bloques como deseemos en sus componentes X, Y, Z. Cuantas más celdas, mayor detalle.
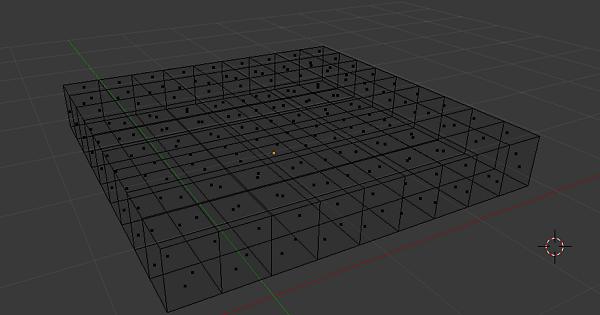
La idea en código:
Vertex3D dimensions = this->bounds.max - this->bounds.min;
float cubeSizeX = dimensions.x / this->numberCubesX;
float cubeSizeY = dimensions.y / this->numberCubesY;
float cubeSizeZ = dimensions.z / this->numberCubesZ;
Vertex3D offsetPosition = Vertex3D::zero();
for (int x = 0; x < numberCubesX; x++) {
for (int y = 0; y < numberCubesY; y++) {
for (int z = 0; z < numberCubesZ; z++) {
auto *cell = new CellGrid();
cell->posX = x;
cell->posY = y;
cell->posZ = z;
cell->box = new AABB3D();
...
...
this->boxes.push_back(cubeGrid);
offsetPosition.z += cubeSizeZ;
}
offsetPosition.z = 0;
offsetPosition.y += cubeSizeY;
}
offsetPosition.y = 0;
offsetPosition.x += cubeSizeX;
}
Llamaremos «celda» a cada cuboide generado y lo indexaremos en base a su posición en el BoudingBox principal, usando también notación X, Y, Z.
struct CellGrid {
AABB3D *box;
int posX;
int posY;
int posZ;
bool is_empty;
};Cada celda almacenará la información que deseemos, en mi caso, cada celda indica simplemente si está vacía o no. La parte negativa del Grid es que hemos de analizar toda la geometría contra cada celda generada, lo cual puede no ser óptimo, la parte buena es que su acceso/lectura es trivial, a través de sus componentes X, Y, Z, algo del tipo:
CellGrid *getCell(int x, int y, int z);
Los Grids son estructuras muy sencillas que pueden ayudarnos a realizar muchísimas tareas de mayor nivel.
Octrees
Los Octrees suponen una evolución respecto al Grid3D. Podemos visualizar de partida un Octree como un Grid de dimensiones 2x2x2, con matices.
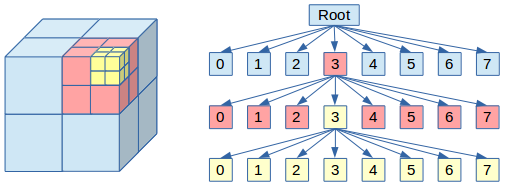
El matiz principal es que un Octree realiza recursivamente esta descomposición del espacio, sobre cada nodo generado, hasta alcanzar un nivel de profundidad dado. A mayor profundidad, mayor detalle.
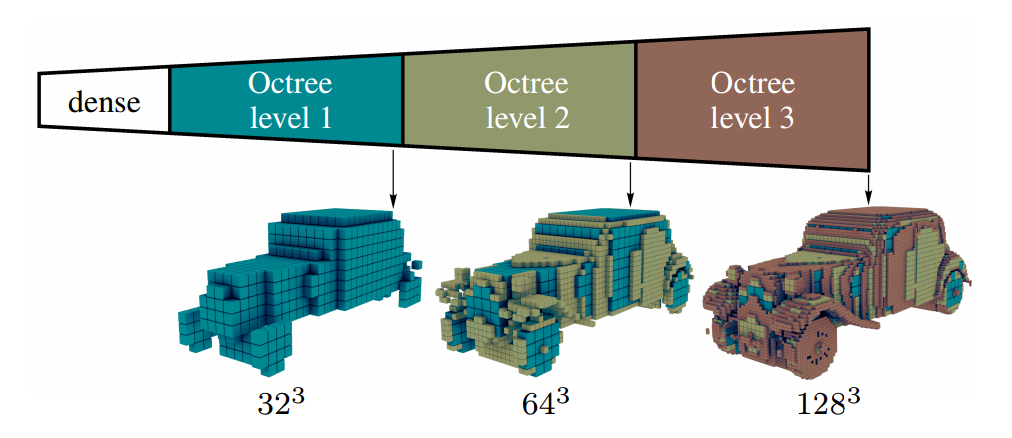
Es una árbol donde cada nodo tiene un máximo de ocho hijos, y así sucesivamente hasta que hayamos alcanzado el mencionado nivel de profundidad, en cuyo caso los nodos se convertirán en hojas sin hijos.
struct OctreeNode
{
AABB3D bounds;
OctreeNode* children[8];
std::vector<Triangle*> triangles;
};
La ventaja principal de un Octree es que no necesita procesar toda la geometría en cada nodo generado, sino que puede limitarse a procesar la geometría aportada por su padre, haciendo que el cálculo de cada nodo de un nivel inferior en el árbol sea más rápido que el anterior. Para determinados volúmenes de geometría, supone una gran optimización respecto al Grid.
La idea en código:
OctreeNode* Octree::BuildOctree(std::vector<Triangle*> &triangles, AABB3D bounds, int recursiveDepth)
{
auto* node = new OctreeNode();
node->bounds = bounds;
for (int j = 0; j < triangles.size(); j++) {
if (isTriangleInsideAABB(triangles[j], bounds)) {
node->triangles.push_back(triangles[j]);
}
}
if (recursiveDepth >= MAX_RECURSIVE_DEPTH) {
for (int i = 0; i < 8; i++) {
node->children[i] = NULL;
}
return node;
}
Vertex3D childSize = (bounds.max - bounds.min);
childSize.getScaled(0.5);
for (int i = 0; i < 8; i++) {
AABB3D childBounds;
Vertex3D childOffset;
switch (i) {
case 0:
childOffset = Vertex3D(0, 0, 0);
break;
case 1:
childOffset = Vertex3D(childSize.x, 0, 0);
break;
...
...
}
childBounds.min = bounds.min + childOffset;
childBounds.max = bounds.min + childOffset + childSize;
node->children[i] = BuildOctree(
node->triangles,
childBounds,
recursiveDepth + 1
);
}
return node;
}
La creación de un Octree es relativamente rápida, con el inconveniente de aumentar ligeramente la dificultad para recorrer el árbol y llegar a nodos deseados a la hora de implementar funciones de mayor nivel
BSP
Los BSP son la estructura más compleja y quizás en desuso de las aquí mencionadas.
Un Octree y un Grid puede descomponer el espacio sin utilizar la geometría, ya que básicamente trabajan con BoundingBoxes, son digamos, una discretización del modelo que representan (pensad en minecraft), sin embargo, un árbol BSP descompondrá el espacio recursivamente utilizando planos de corte. Los árboles BSP suelen utilizados para almacenar una geometría al detalle, mientras que los Octrees y Grids salen perdiendo en este aspecto.
Su explicación en sí no es compleja: Se trata de elegir un plano perteneciente a la geometría y partirla en dos en base a dicho plano, generando dos nodos. Con cada nodo haremos lo mismo recursivamente hasta que no haya más planos que separar y estemos ante nodos hoja. En un árbol BSP las hojas representarán los espacios vacíos.
Una imagen vale más que mil palabras. A continuación podéis ver un ejemplo de las iteraciones a la hora de construir un árbol BSP, usando de ejemplo un mapa de Doom:
- Selecciona un plano de corte:
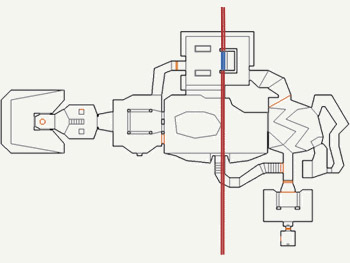
2) El plano anteriormente seleccionado parte el espacio en dos mitades:
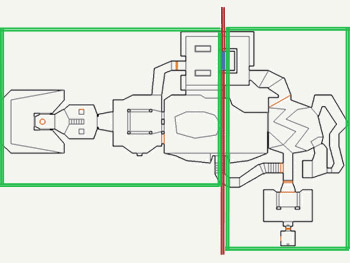
3) Iteramos sobre las mitades generadas anteriormente, seleccionando un nuevo plano de corte en cada una de ellas:
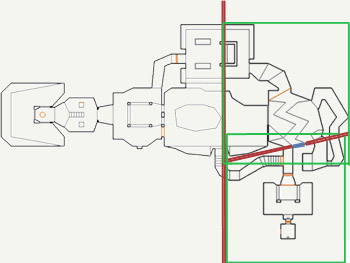
4) Así sucevisamente hasta el final, donde llegaríamos a disponer de toda la información de la geometría:
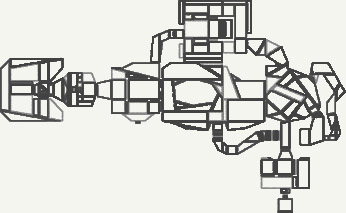
A continuación un ejemplo del código de lo que podría representar un nodo y una hoja de un árbol BSP:
struct dnode_t
{
int planenum;
short children[2] = {};
short mins[3];
short maxs[3];
unsigned short firstsurf;
unsigned short numsurf;
};
struct dleaf_t
{
int contents = 0;
int vislist;
short mins[3];
short maxs[3];
short firstsurf;
short numsurf;
};
Nótese como almacenan los BoundingBox de cada nodo, aunque no es estrictamente necesario en una estructura BSP, pero es una forma de matar dos pájaros de un tiro, disponiendo de una discretización de la geometría muy útil para funcionalidades de mayor nivel.
La implementación de un BSP está plagada de detalles y estructuras de apoyo. Hay que tener en cuenta que hemos de almacenar todos los planos, vértices, superficies, etc. Sugiero echar un vistazo completo al fichero BSPMap.h si deseáis conocer más detalles acerca del mismo.
Una de las preocupaciones a la hora de crear un árbol BSP será precisamente equilibrarlo. Ya que en función de los planos de corte elegidos para crear los nodos, el árbol BSP puede quedar muy desbalanceado. Habrá que calcular cual es el plano de corte más adecuado para seguir procesando cada nodo. Intentaremos que sea un plano en «la mitad» de cada nodo, precisamente para balancearlo. Existen distintas estrategias en la selección del plano de corte, bien podríamos crear un plano según nuestras necesidades, aunque tendríamos que recortar la geometría, o limitarnos a usar los planos exactos de la geometría ya existente, lo cual sería una comodidad a mi forma de ver. A continuación algunos ejemplos:
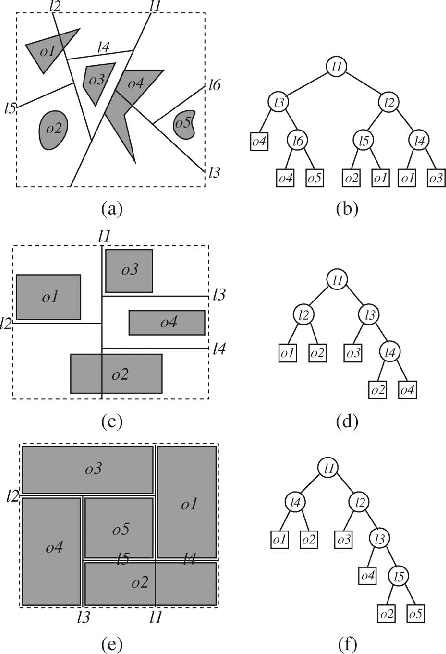
Ya en tiempo de ejecución nesitarémos recorrer un árbol BSP: Comenzaremos desde su nodo raíz determinando en qué mitad del espacio nos encontramos. Cómo cada nodo tiene dos hijos, cada hijo representa una de esas mitades, si no es una, será la otra. Una vez sepamos en qué mitad nos encontramos, repetimos recursivamente dicha operación con el nodo que representa esa mitad, hasta que no haya más hijos que procesar.
La forma de determinar en qué mitad de un nodo se encuentra un punto en el espacio será utilizando la función «distancia plano vs punto«, la cual nos aporta un valor positivo o negativo en función de si el punto cae en frentre o detrás del plano de corte en cuestión:
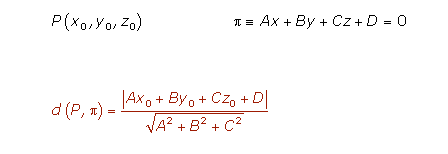
La idea principal es que si estás en un nodo no estás en otro, por lo que podrás descartar la geometría de todos aquellos nodos que no sea en el que se encuentra la cámara. Ciertamente esto tiene matices, si la cámara se encuentra apuntando desde un nodo hacia otro, posiblemente debamos procesar ambos nodos.

Intentaré explicarlo con un ejemplo: imaginemos una vivienda en 3D, donde cada habitación será un nodo y el pasillo que las conecta, otro nodo. No es difícil ver que desde el pasillo podemos estar alcanzando a visualizar el interior de una o más habitaciones simultáneamente, es decir, necesitas la información de todos estos nodos. Necesitamos una solución específica para estos casos, evitando el uso de «la fuerza bruta» procesando todos los nodos involucrados en el render. ¿Cómo se alivia este problema habitualmente?. Lo analizamos a continuación.
Conjuntos potencialmente visibles (PVS)
El es un problema con varias soluciones, sin embargo, voy a destacar la que siempre me he encontrado con los BSP: Los conjuntos potencialmente visibles (PVS): Son otras estructuras de datos anexas al BSP en la que se almacena toda la geometría visible desde cada nodo. Su creación es muy costosa, ya que para su determinar esta información hay que lanzar un montón de rayos y/o barridos . Cómo os podéis imaginar el resultado es una estructura de información enorme.
En contra de lo que pueda parecer, leer un PVS en tiempo real, suele ser una estrategia más eficaz que enviar al render toda la geometría de los nodos que pudieran verse involucrados en la cámara, para descartar finalmente la gran mayoría, probablemente.
Esta solución fue la que hizo posible hace décadas mover entornos 3D en «tiempo real» con muy poca potencia (486, Pentium..), básicamente la realización de un pre-cacheo brutal de información que evitase al render lidiar con toda esa geometría. Cabe destacar que hoy en día todo este esfuerzo es absurdo si lo comparamos con un render basado en GPU, el cual será capaz de descartar toda la geometría por hardware siempre más rápido que nuestra mejor solución, siempre!
Además las soluciones de renderizado basadas en BSP/PSV tienen un punto débil muy conocido: Su limitación para funcionar bien con grandes espacios abiertos, mientras que por el contrario funciona genial para geometrías «pasilleras» con habitaciones y recovecos. Podéis imaginar que las estructura PSV para una geometría con recovecos serán pequeñas y manejables, sin embargo los espacios abiertos tendrán que gestionar estructuras PSV inmensas ralentizando su renderizado.
Resumen
Hemos presentado tres estructuras de datos muy conocidas en el mundillo del 3D, cuyo uso dependerá exactamente de nuestro ingenio y necesidades para desarrollar funcionalidades de mayor nivel.
En el futuro nos apoyaremos en alguna, sino en varias simultáneamente para alcanzar más objetivos.






Deja una respuesta