Implementar Billboards en un engine 3D

Buenas a todos!. En el último artículo aprendimos la importancia del winding-order en el procesado de los triángulos de nuestra escena. Hoy vamos a resolver otro de los problemas más habituales en nuestra misión de crear un motor: Cómo implementar billboards en un engine 3D.

Los billboards, no son más que elementos 2D incrustados en nuestro mundo 3D. En la práctica, sirven para incorporar efectos a nuestro motor, ya sean partículas como el fuego o el humo, además del posicionamiento de iconos en nuestro entorno 3D a modo de guía. Veámos un ejemplo en movimiento:

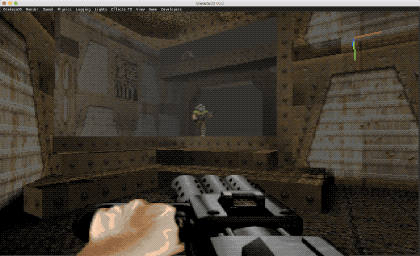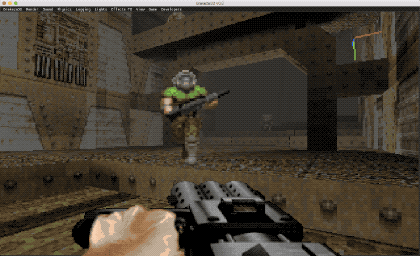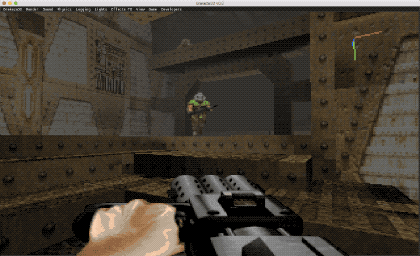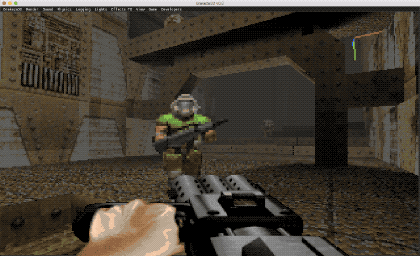
Como podéis observar en la imagen superior, el “DoomGuy” del DOOM es una imagen 2D, ya que físicamente es un PNG (en este caso varias, al tratarse de una animación), sin embargo, se integra perfectamente con el motor, adaptándose el sprite a un mundo 3D. El comportamiento del billboard puede variar según nuestras necesidades, más adelante analizaremos algunos de los casos más habituales.

Existen diferentes mecanismos para implementar billboards en un engine 3D, a bote pronto se me ocurren dos grandes bloques:

• Aproximaciones 2D: Aquellas en las que superpondremos en pantalla (XY) los sprites en alguna fase del renderizado. En función de la distancia a la cámara, variaríamos el tamaño del sprite 2D en pantalla. Este enfoque tiene ciertas limitaciones, pero en la práctica funciona.
• Aproximaciones 3D: Crearemos los triángulos en la escena que darán soporte a nuestro billboard, los texturizaremos y los mantendremos perfectamente alineados con nuestra cámara según nuestras necesidades. En mi opinión la solución definitiva. Este es el sistema adoptado por Brakeza3D y que detallaremos a continuación.

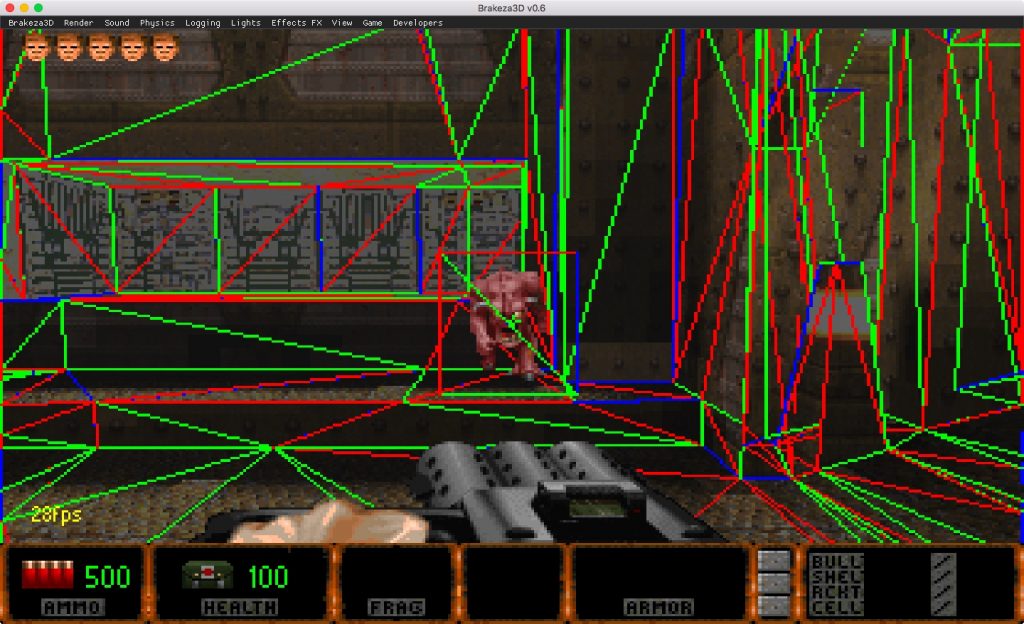
Si observamos el wireframe de la imagen superior, observamos que nuestro “demon” está formado por dos triángulos (aproximación 3D),  sin embargo la metralleta no está formada por triángulos (aproximación 2D)

El primer objetivo para implementar nuestro billboard, será por tanto, el averiguar cuales son estos dos triángulos, a continuación mapearemos las coordenadas UV de los vértices de estos triángulos. Además aprenderemos a colocar estos triángulos en el espacio para que siempre encaren a la cámara según nuestras necesidades.

Una vez hayamos averiguado toda esta información, simplemente enviaremos los dos triángulos al pipeline de rasterización.

Posición respecto al observador

Como ya os adelante, el comportamiento del billboard respecto a la cámara puede variar según nuestras necesidades. Se me ocurren dos situaciones:

• Billboard sin restricciones: Nuestro billboard rotará en cualquier eje para situarse siempre alineado a nuestra cámara. Este tipo de billboard es el habitual para conseguir efectos tipo humo o enemigos del estilo del Duke Nukem o DooM.
• Billboard con restricciones: Si entendemos el ejemplo anterior, no tenemos más que imaginarnos alguna limitación en la rotación en cualquiera de los ejes.

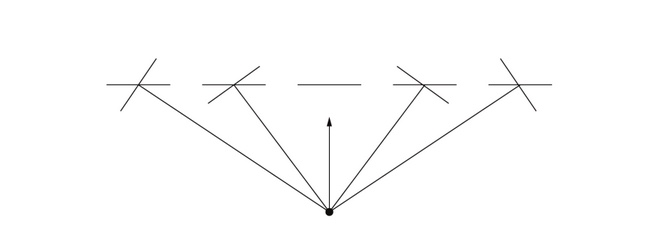
En la imágen superior podéis ver que los triángulos variarán si existe alguna restricción en su rotación (el punto sería la cámara). Por ahora vamos a centrarnos en la implementación del sistema de billboard sin restricciones que he utilizado en Brakeza3D.

Ingredientes

Para calcular los vértices de los triángulos que conformarán nuestro billboard, primero hemos de tener claro los datos que determinan un billboard:

• Posición 3D: Posición del centro del billboard en el espacio.
• Alto: Alto del billboard.
• Ancho: Ancho del billboard.
• Cuatro vértices: Con la posición, el alto y ancho, calcularemos cuatro vértices que convertiremos en dos triángulos.
• Textura: Aprenderemos a incorporar las coordenadas UV a los vértices de nuestros triángulos.

El primer paso será calcular los cuatro vértices del “cuadrado” de nuestro billboard. Si leísteis el artículo sobre el frustum, veréis que son cálculos similares a los planos farPlane y NearPlane.

A continuación el código de como podemos obtener los cuatro vértices (Q1, Q2, Q3 y Q4) utilizando la posición del objeto y dos vectores (Up y Right) para mantener el billboard alineado a ellos. Los vectores Up y Right se corresponden con los de la rotación de la cámara.

void Billboard::unconstrainedQuad(Object3D *o, Vertex U, Vertex R)
{
    Vertex X;
    X.x = (width/2) * R.x;
    X.y = (width/2) * R.y;
    X.z = (width/2) * R.z;

    Vertex Y;
    Y.x = (height/2) * U.x;
    Y.y = (height/2) * U.y;
    Y.z = (height/2) * U.z;

    Q1.x = o->getPosition()->x + X.x + Y.x;
    Q1.y = o->getPosition()->y + X.y + Y.y;
    Q1.z = o->getPosition()->z + X.z + Y.z;

    Q2.x = o->getPosition()->x - X.x + Y.x;
    Q2.y = o->getPosition()->y - X.y + Y.y;
    Q2.z = o->getPosition()->z - X.z + Y.z;

    Q3.x = o->getPosition()->x - X.x - Y.x;
    Q3.y = o->getPosition()->y - X.y - Y.y;
    Q3.z = o->getPosition()->z - X.z - Y.z;

    Q4.x = o->getPosition()->x + X.x - Y.x;
    Q4.y = o->getPosition()->y + X.y - Y.y;
    Q4.z = o->getPosition()->z + X.z - Y.z;

    Q1 = Transforms::objectToLocal(Q1, o);
    Q2 = Transforms::objectToLocal(Q2, o);
    Q3 = Transforms::objectToLocal(Q3, o);
    Q4 = Transforms::objectToLocal(Q4, o);

    Q1.u = 1.0f; Q1.v = 1.0f;
    Q2.u = 0;    Q2.v = 1.0f;
    Q3.u = 0;    Q3.v = 0;
    Q4.u = 1.0f; Q4.v = 0;

    T1 = Triangle(Q3, Q2, Q1, o);
    T2 = Triangle(Q4, Q3, Q1, o);
}

Cabe destacar que las coordenadas que estámos calculando para Q1-Q4 son coordenadas de mundo, es decir, posiciones absolutas en el mundo 3D. Ya que nos interesará manejar nuestro billboard como si de un objeto 3D más se tratase, convertimos las coordenadas de mundo a coordenadas del objeto, es decir, coordenadas locales.

Os invito a refrescar las transformaciones de vértices en el artículo en que creámos nuestra primera cámara. A continuación las líneas que en resumen resuelven este problema (en GitHub podéis revisar las transformaciones):

Q1 = Transforms::objectToLocal(Q1, o);
Q2 = Transforms::objectToLocal(Q2, o);
Q3 = Transforms::objectToLocal(Q3, o);
Q4 = Transforms::objectToLocal(Q4, o);

Mapeado UV

El objetivo del billboard es dibujar una imagen y la vamos a tratar como una textura normal y corriente.

Como único inconveniente sería el tratamiento de las transparencias. Brakeza3D incluye texturas con canal ALPHA, es decir, tiene en cuenta este canal de color para decidir el color final del pixel (mediante alpha blends). Esto no es obligatorio para entender los rudimentos de los billboards, pero asumo que no siempre querréis billboards “cuadrados”, será necesario incorporar la gestión del canal alpha a vuestro rasterizador.

Volviendo a el mapeado UV, si sabemos que vamos a formar dos triángulos que cubran toda nuestra imagen y que las coordenadas UV son valores que oscilan en un rango [0, 1] podemos concluir que:

Q1.u = 1.0f; Q1.v = 1.0f;
Q2.u = 0;    Q2.v = 1.0f;
Q3.u = 0;    Q3.v = 0;
Q4.u = 1.0f; Q4.v = 0;

Podéis repasar los conceptos sobre el mapeado UV en el artículo que hablamos de texturas.

Creando los triángulos

Llegados a este punto tenemos todo lo necesario para crear los triángulos y enviarlos a nuestra pipeline de renderizado.

T1 = Triangle(Q3, Q2, Q1, o);
T2 = Triangle(Q4, Q3, Q1, o);

Simplemente combinamos nuestros cuatro vértices adecuadamente para formar dos triángulos.

No olvidéis que hemos de actualizar nuestros billboards en el espacio constantemente respecto a la posición y rotación de la cámara, asi que como mínimo repetiremos estos cálculos cada vez que la cámara se mueva por la escena.

Resumen

Te mostramos cómo implementar billboards en un engine 3D, un mecanismo para situar elementos 2D en escena. Si dotamos a nuestro rasterizador de una correcta gestión del canal alpha, podremos utilizar esta técnica para añadir multitud de efectos a nuestra escena, ya sea una interfaz gráfica, enemigos, iconografía, etc. Nos vemos en el siguiente artículo!